数学(20)

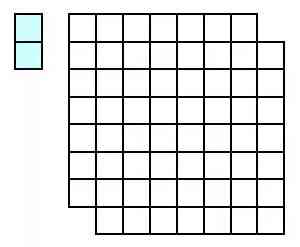
我们常把上面左图所示的这种1×2的小长方形叫做一个多米诺骨牌。给你足够的多米诺骨牌，你能用它们既无重复又无遗漏地铺满右图所示的棋盘吗？每个多米诺骨牌既能橫着放也能竖着放。您不妨先自己思考几分钟，然后再阅读。

某次会议一共有100个人参加，其中某些人之间握过手，但每两个人之间最多只会握一次手。会议结束后，不同的人握手的次数不同，有的人握手次数少，有些人握数次数多。问：是否一定能找到两个人，他们握手的次数是相同的？您不妨先自己思考几分钟，然后再阅读。

在维基百科是这样介绍芝诺悖论的：

芝诺悖论是古希腊数学家芝诺（Zeno of Elea）（盛年约在公元前464-前461）提出的一系列关于运动的不可分性的哲学悖论。这些悖论由于被记录在亚里士多德的《物理学》一书中而为后人所知。芝诺提出这些悖论是为了支持他老师巴门尼德关于“存在”不动、是一的学说。这些悖论是芝诺反对存在运动的论证其中最著名的两个是：“阿基里斯追乌龟”和“飞矢不动”。

下面是我之前的笔记，整理如下。 

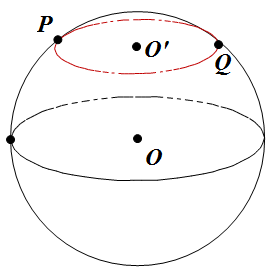
平面上两点最短距离大家都知道直线最短，这是公理，因为这连牛都知道（小牛肯定优先选择直线跑向牛妈）。但是球面两点最短距离就不是凭直觉可以知道的了。 比如下图 P、Q 两点的最短距离是大圆 O 上的劣弧，还是小圆 O'上的劣弧，还是其它弧呢？注：劣弧指的是两段弧中较短的弧。 

上一篇 球面两点最短距离 证明了球面两点最短距离是和球心形成的大圆的劣弧。我们利用这一结论，可以用于计算地球上两地间的最短距离。我们可以把地球看作一个标准的球体，两地间没有障碍物，不会高低不平，这样看来就特别适用于航海。而在陆地上我们可以做为一个参考距离。

问题1：证明对任意一个闭曲线，总存在一条直线把它分成面积相等的两份。

图1

最近考上南京邮电大学的徐玉玉学费被骗身亡，清华教授被骗1760万，暴露了很多问题，比如银行系统/制度的漏洞，我们的身份、隐私泄漏问题。今天早上想到下面这么个问题。

小明和小白在火车上相遇，聊得很投缘。小明想知道自己的生日和小白是否相同，但是由于刚刚认识，想尽量保护双方的隐私（能满足如果生日不一样不希望对方知道自己的生日即可）。请你给他们出一个方案。

一场活动要测试鸵鸟蛋的坚固性。要让蛋从高楼上落下而不破，进而依据不破的最高楼层决定蛋的硬度。测试的高楼共101层。测试员意识到，如果他只带一颗鸵鸟蛋的话，他需要从第1层开始往上依次每一层把蛋投下以判定蛋的硬度。

如果他带两颗鸵鸟蛋（假定坚固性一样），那么在最坏的情况下他需要测试多少次呢？

一个点在x 轴行走，起始点在原点，每次走 1 格，每次的方向随机或正或负，概率均为1/2。行走 n 步后，预期该点相对原点的绝对距离是多少呢？

这是前几年的随笔，分享下。一家人带着不到三岁的女儿在厦门科技馆玩耍。 在科技馆玩了一天，最后一个项目是女儿自己进入和小朋友们一起玩，大人在外面等候。

我们先聊生日悖论问题，后面再看看什么是生日攻击。

傅里叶变换

\begin{align*} \widehat{f}(w) =& \int_{-\infty}^{+\infty} f(x) e^{-ixw} dx \\ =&\int_{-\infty}^{+\infty} f(x) (\cos wx - i\sin wx) dx \\ =& \int_{-\infty}^{+\infty} f(x) \cos wx dx  - i \int_{-\infty}^{+\infty} f(x) \sin wx dx \qquad (1) \end{align*}

如果一个随机变量具有概率密度函数

\begin{align*} f(x)=\frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty \end{align*}

则称X为正态随机变量并记为$X \sim N(\mu, \sigma^2)$．这里N 为“Normal” 一词的首字母．$\mu, \sigma$ 都是常数，$\mu$ 为均值，可以取任何实数值, 而$0 < \sigma^2 < \infty$ 为方差，$\sigma$ 称为标准差。这种分布我们称之为正态分布，德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布。

古希腊哲学家苏格拉底曾言：“我唯一知道的就是我一无所知。”； 中国儒家学派创始人孔子曰：“知之为知之，不知为不知，是知也。”； 德国著名数学家希尔伯特则满怀信心地说道：“我们必须知道，我们必将知道。” 。我觉得希尔伯特和苏格拉底、孔子的说法并不矛盾，因为只有当你知道自己不知道时，才会去探寻，才会说“我们必须知道，我们必将知道”。

这是伯克利2013年秋数学博士资格的一道数论题。令 m=561，若 a 与m互素，证明

\[a^{m-1} \equiv 1 \pmod{m} .\]

如下图，看图列式计算，这是一道求部分的题。我发现对于这类题，我女儿经常写成加法， 3+6=9，下面是我提醒她修改后的。

在计算机中，字符可以进行大小比较，ASCCI码字符大小关系如图(ASCCI码字符大小)，和数轴类似，左边的字符小于右边的字符。而字符串由字符组成，因此简单的字符串排序方法，可以逐字符进行大小比较排序。

ASCCI码字符大小

例如 a9.txt, a10.txt, 假设按字符升序逐个排序，则排序的结果为a10.txt, a9.txt。第1个字符双方都是'a'，大小相等；由于按升序排序，第2个字符'1'排在字符'9'前面，即'1'<'9'，因此'a1'排在'a9'前面，后面就不需要再继续比较了。

在数学345视频号第14期《对称》中我们讲到了镜像对称。镜像对称可以通过镜像变换实现。镜像变换通常是关于某个轴或直线做翻转操作操作。 在图像处理中，常见的是水平镜像和垂直镜像。

水平镜像是关于垂直中轴线的镜像，即图像沿着垂直中轴线左右翻转。如下图：

晚上陪女儿到图书馆看书写作业，顺便做了下2024新课标I卷数学高考压轴题。当时写在餐巾纸上，晚上洗完澡整理成文字如下：

19. 设 $m$ 为正整数，数列 $a_1, a_2, \cdots, a_{4 m+2}$ 是公差不为 0 的等差数列, 若从中删去两项 $a_i$ 和 $a_j(i<j)$ 后剩余的 $4 m$ 项可被平均分为 $m$ 组, 且每组的 4 个数都能构成等差数列, 则称数列 $a_1, a_2, \cdots, a_{4 m+2}$ 是 $(i, j)$ 一一可分数列.

（1）写出所有的 $(i, j), 1 \leq i<j \leq 6$, 使数列 $a_1, a_2, \cdots, a_6$ 是 $(i, j)$ 一一可分数列；

（2）当 $m \geq 3$ 时，证明：数列 $a_1, a_2, \cdots, a_{4 m+2}$ 是 $(2,13)$ 一一可分数列;

(3) 从 $1,2, \cdots, 4 m+2$ 中一次任取两个数 $i$ 和 $j(i<j)$, 记数列 $a_1, a_2, \cdots, a_{4 n+2}$ 是 $(i, j)$ 一一可分数列的概率为 $P_m$, 证明: $P_m>\frac{1}{8}$.

早上一老同学微信发我今年福建的中考数学题。上午没时间，女儿中午要吃汉堡烤鸡，店里借了笔，在餐巾纸中写了下。其实没什么难度，而且第二小题，还可以进一步缩小已知条件。发到朋友圈后，有同事建议我发给ChatGPT做，测试看看。

已知，实数 a, b, c, m, n 均满足 $3m+n=\frac{b}{a}, mn=\frac{c}{a},$

(1)求证: $b^2 - 12ac \ge 0$

(2)若a,b,c均为奇数，m,n是否有可能都是整数，请说明理由。