古希腊哲学家苏格拉底曾言：“我唯一知道的就是我一无所知。”； 中国儒家学派创始人孔子曰：“知之为知之，不知为不知，是知也。”； 德国著名数学家希尔伯特则满怀信心地说道：“我们必须知道，我们必将知道。” 。我觉得希尔伯特和苏格拉底、孔子的说法并不矛盾，因为只有当你知道自己不知道时，才会去探寻，才会说“我们必须知道，我们必将知道”。

欧拉在发现欧拉函数、欧拉定理时，肯定不知道他发现的这些东西会成为当代计算机密码学中非对称秘钥RSA的基石。英国著名数学家哈代（华罗庚的导师）也不知道，甚至他认为这些定理大都是无用的。他甚至在《一个数学家的辩白》中自豪地宣称: “真正”的数学家所研究的“真正”的数学，如费马、欧拉、高斯和阿贝尔所研究的数学，几乎是完全“无用”的。.... 我从未做过任何一件“有用的事”。我的新发现未曾，且将来也不大可能为世界增加哪怕是最限度的舒适感，不论是直接的还是间接的，也不管是善意的还足恶意的，都做不到这一点。我也曾培训过其他数学家，但这些人与我是同样类型的数学家，他们所做的工作也同我做的工作一样没有用处。若是以实用的标准来作评判的话，我的数学生命的价值是零;从数学之外看来，我的价值无论如何也是微不足道的。我只有一种机会免被判断为完全微不足道，那就是人们可能判定我已做出了一些有创造价值的工作。 我不否认，我已做了一些创造性的工作，问题是它们的价值怎样。

显然哈代错了。欧拉函数、欧拉定理已成为当代计算机密码学中非对称秘钥RSA的基石。我们现在浏览网页、购物等等的安全性大都依赖非对称密码方案。而RSA密码方案(有时也称为Rivest-Shamir-Adleman算法)是目前使用最广泛的一种非对称密码方案，当然椭圆曲线和离散对数方案也逐渐普及。

RSA算法是 Ronald Rivest, Adi Shamir 和Leonard Adleman 在1977 年提出的。RSA应用非常广泛，在实际中常用于：

1. 加密小片段的数据，比如用于密钥传输.

2. 数字签名，比如数字证书。

需要注意的是，RSA比对称加密(例如AES)要慢很多。这主要是因为RSA执行中涉及到大量计算。因此，RSA并不是为了取代对称密码。RSA的一个主要用途就是安全地交换对称密码的密钥（即密钥传输)。实际上，RSA通常与类似AES的对称密码一起使用，其中真正用来加密大量数据的是对称密码。

RSA的安全性主要是建立在整数因式分解问题上：两个大素数相乘在计算上是非常简单的(人们使用笔和纸就能完成)，但是对其乘积结果进行因式分解却是非常困难的。欧拉函数和欧拉定理在RSA中发挥着至关重要的作用。下面我们将先将讲述欧拉函数、欧拉定理，最后再介绍RSA。

欧拉函数

欧拉函数考虑的是互素个数问题。

欧拉函数：当 m 为大于1的整数时，用$\varphi(m)$ 表示$1,2, \dots, m$ 中与m 互素的正整数个数，则

\[\varphi(m) = m(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots (1-\frac{1}{p_k}) \tag{1}\]

其中 $p_1, p_2, \dots, p_k$ 为 m 的所有互异的素因数。

重新看这个问题的时候，我想到了一个更简单的证明方法。欧拉函数(1) 式可以化为

\[\varphi(m) = \frac{m}{p_1p_2 \dots p_k} (p_1-1)(p_2-1)\dots (p_k-1) . \tag{2}\]

这个式子可以理解为有 $\frac{m}{p_1p_2 \dots p_k}$ 个区间，区间的大小为 $p_1p_2 \dots p_k$ 。只要证明每个区间都有 $(p_1-1)(p_2-2)\dots (p_k-1)$ 个数和 m 互素即可。

引理1 如果 $m=p_1p_2\dots p_k$ ，则

\[\varphi(m) = (p_1-1)(p_2-1) \dots (p_k -1) . \tag{3}\]

不妨设 $p_1 < p_2 < \dots < p_k$ ，当k=1时显然成立， 因为当 p 为素数时$\varphi(p)=p-1$。

当 k=2 时，$\varphi(p_1p_2)$ 可以这样计算，我们从 $\varphi(p_1)$ 个数中任意取一个数，不妨记为 a ，$(a,p_1) = 1$ ，然后通过 a 生成下面这些数

\[a + 0p_1, a + p_1, a + 2p_1, \dots , a + (p_2-1)p_1 \tag{4}\]

由于 $(p_1,p_2)=1$ ，根据“互素时剩余类的性质”，可知 $0,p_1,2p_1,\dots,(p_2-1)p_1$ 模$p_2$ 构成的集合恰好为 $0,1,2,\dots,p_2-1$ 。 不论 a 为多少，(4) 式必定恰好有1个数可以整除 $p_2$ ，其余均和 $p_2$ 互素。 即从 a 生成出来的这些数中，恰好有 $p_2-1$ 个数和$p_1, p_2$ 都互素。由于 a 的个数等于 $\varphi(p_1) = p_1 - 1$，所以

\[\varphi(m = p_1p_2) = (p_1-1)(p_2-1) .\]

当 k = 3 时，类似证明。 从 $\varphi(p_1p_2)$ 个数中任意取一个数，不妨记为 a ，$(a,p_1p_2) = 1$ ，然后通过 a 生成下面这些数

\[a + 0p_1p_2, a + p_1p_2, a + 2p_1p_2, \dots , a + (p_3-1)p_1p_2 \tag{5}\]

由于 $(p_1p_2, p_3)=1$ ，根据“互素时剩余类的性质”，可知 $0,p_1p_2,2p_1p_2,\dots,(p_3-1)p_1p_2$ 模$p_3$ 构成的集合恰好为 $0,1,2,\dots,p_3-1$ 。不论 a 为多少，(5) 式必定恰好有1个数可以整除 $p_3$ ，其余均和 $p_3$ 互素。 即从 a 生成出来的这些数中，恰好有 $p_3-1$ 个数和$p_1p_2, p_3$ 都互素。由于 a 的个数等于 $\varphi(p_1p_2) = (p_1 - 1)(p_2-1)$，所以

\[\varphi(m = p_1p_2p_3) = (p_1-1)(p_2-1)(p_3-1) .\]

依次类推，可知引理1成立。

欧拉函数证明: 当 $m = p_1^{a_1}p_2^{a_2}\dots p_k^{a_k}$ ，我们需要考察区间

\[ [i(p_1p_2\dots p_k)+1, \quad (i+1)(p_1p_2\dots p_k) ] , \quad ( i \ge 0)\]

和 m 互素的个数。

由引理1知，当 i = 0 时， $[1,p_1p_2 \dots p_k]$ 区间满足 $(a, p_1p_2 \dots p_k) = 1$ 的 a 恰好有 $(p_1-1)(p_2-1)\dots (p_k-1)$ 个。这些 a 也满足 $(a, m) = 1$ ，否则必定存在某 $p_j$ 成立 $p_j | (a, m)$ ，可推出 $p_j | a$ ，这和 $(a, p_1p_2 \dots p_k) = 1$ 矛盾。

当 i> 0 时，显然有 $(a + i(p_1p_2 \dots p_k), p_1p_2 \dots p_k) = 1$ 。 同样 $(a + i(p_1p_2 \dots p_k), m) = 1$ ，否则必定存在存在某 $p_j$ 成立 $p_j | (a + i(p_1p_2 \dots p_k), m)$ ，可推出 $p_j | a$ ，这和 $(a, p_1p_2 \dots p_k) = 1$ 矛盾。

因此不论 i 是多少，对于任意区间都恰好存在

\[(p_1-1)(p_2-1)\dots (p_k -1)\]

个数和 m 互素。

综上，便得到欧拉函数。

证毕。

欧拉定理

设 m 为正整数， a 为任意整数，且(a,m)=1, 则

\[a^{\varphi(m)} \equiv 1 \pmod{m} \]

其中 $\varphi(m)$ 为欧拉函数表示$1,2, \dots, m$ 中与m 互素的正整数个数。

显然这是费马小定理的推广，费马小定理只是该定理的一个特殊情形。

证明： 设和 m 互素的数分别为 $p_1<p_2<\dots<p_{\varphi(m)}$. 根据“互素时剩余类的性质” ，由于$(a, m) = 1$, 且$1 \le p_1,p_2,\dots, p_{\varphi_{m}} < m$ ，所以 $ap_1,ap_2, \dots, ap_{\varphi(m)}$ 必定模m两两不同余 。

$ap_1, ap_2, \dots, ap_{\varphi(m)}$ 共 $\varphi(m)$ 个，两两不同余，每一个都还和 m 互素，则他们的余数的集合必定刚好就是 $\{p_1,p_2,\dots,p_{\varphi(m)}\}$，所以

\begin{align*} ap_1\cdot ap_2 \cdot \dots \cdot ap_{\varphi(m)} \equiv p_1\cdot p_2\cdot \dots \cdot p_{\varphi(m)} \pmod{m} \end{align*}

又

\[ (p_1\cdot p_2\cdot \dots \cdot p_{\varphi(m)}, m) = 1\]

消去, 得

\[a^{\varphi(m)} \equiv 1 \pmod{m} \]

证毕。

RSA 加解密

公钥$ k_{public} = \{n, e\}$, 对明文x加密

\[y \equiv x^e \pmod{n} \tag{1}\]

私钥$k_{private} = \{n, d\} $, 对密文y解密

\[x \equiv y^d \pmod{n} \tag{2}\]

其中$n=pq$ (p,q为素数), e,d 满足下面的关系

\begin{align*} gcd(e, \varphi(n)) = 1, de \equiv 1 \pmod{\varphi(n)} \end{align*}

注: $\varphi(n)$ 为欧拉函数。

由于$gcd(e, \varphi(n)) = 1$，所以e模$\varphi(n)$的逆元d必定存在且唯一。我们只需要证明密文y经过(2)式运算后确实能得到x。

证明 由于

\[y  \equiv x^e \pmod{n} ,\]

所以只需要证明

\begin{align*} x =& (x^{e})^d \mod{n} \\ =& x^{ed}\mod{n} \end{align*}

根据密钥生成的约束，私钥 d 为 公钥$\{e,n\}$ 指数 e 模 $\varphi(n)$ 的逆元，即

\[de \equiv 1 \pmod{\varphi(n)} .\]

因此, de 可表示为

\[de = 1 + k\varphi(n),\]

代入，得

\begin{align*} x^{ed} = x^{1+k\varphi(n)} = x (x^{\varphi(n)})^k \end{align*}

(1)当 $gcd(x, n)=1$ 时，根据欧拉定理

\[x^{\varphi(n)} \equiv 1 \pmod{n},\]

所以

\[x^{ed} \equiv x \pmod{n} .\]

由于 $0 \le x < n$，所以

\[x = x^{ed} \mod{n} .\]

(2)当 $gcd(x, n) \neq 1$ 时，由于$gcd(x, n) \neq 1$，必有

\[x=rp \text{或} x=sq \quad (r,s\text{为整数})\]

不妨设 $x=rp$，可知 $gcd(x,q)=1$ .

又因为$\varphi(n)=(p-1)(q-1)$，所以

\[(x^{\varphi(n)})^k = (x^{(p-1)(q-1)})^k = (x^{q-1})^{k(p-1)}\]

由欧拉定理知 $x^{q-1} \equiv 1 \pmod{q}$，所以

\[(x^{\varphi(n)})^k  \equiv 1 \pmod{q}\]

于是 $(x^{\varphi(n)})^k = 1+ uq$, 代入

\begin{align*} x^{ed} =& x (x^{\varphi(n)})^k =x(1+uq) \\ =& x + uxq = x + urpq \\ =&x+urn\end{align*}

所以

\[x^{ed} \equiv x \pmod{n} \]

证毕。

为什么 n 要取两个大素数p,q 的乘积？ 

换个角度，n 取一个大素数可行吗？n 取3个或更多个大素数的乘积可行吗？

略加思考后，便可得到答案。

1. n 取一个大素数不可行。理由是由上面的证明可知, 当 $0 \le x < n$ 时，必定有 $gcd(x, n)=1$，可知(2) 式解密必定成立。但是 n 是公钥n和e的一部分, 攻击者可以由 n 知 $\varphi(n)=n-1$ ，从而非常容易计算出私钥 e。

2. n 取3个或更多个大素数的乘积也不太可行。因为需要替换上面(2)中的证明，一般来说不太可能成立。除非保证$gcd(x, n)=1$ 一定成立，即保证x小于n 的任意一个素因数。但是如果x的范围越小，被破解的可能性就越大。

破解的难度

现在我们尝试破解RSA加密算法，看看困难在哪里。由于共钥n,e 是公开的，所以实际上我们只需要知道私钥n,d中的d即可。而d是e模$\varphi(n)$的逆元。求逆元是很简单的，关键在于怎么快速地算出以n为参数的欧拉函数$\varphi(n)$ ? 如果我们知道了n的因式分解 n=pq, 根据欧拉定理便能立即计算出$\varphi(n)$。可是如果 n 是一个很大的数的话，目前我们没有一个好的算法可以让计算机在短时间内分解出来。这就是教科书上经常说的一句话：两个大素数相乘在计算上是非常简单的，但是对其乘积结果进行因式分解却是非常困难的。目前也没有找到其它算法能快速地计算出欧拉函数$\varphi(n)$ 。

加密和签名场景别搞混了

从上面证明的过程不难看成，e和d 的地位是相等的，理论上 e 和 d 交换是没有问题的。上面也提到RSA 主要有2种场景，一种是加密(一般用于对称秘钥的传输)，另外一种是签名。加密采用公钥，解密使用私钥。那么签名呢？签名的思路是使用私钥对明文的hash值进行加密，明文本身没有加密(因为签名的目的是防止抵赖)，使用公钥解密得到hash-decrypt值，再对收到的明文使用相同的hash函数计算得到hash-calc值，比较 hash-decrypt 和 hash-calc 值是否一致， 如果一致那么可以断定是使用该公钥对应的私钥进行签名的。不对明文直接加解密，而是对 hash 值，主要是出于计算开销和安全性的考虑。

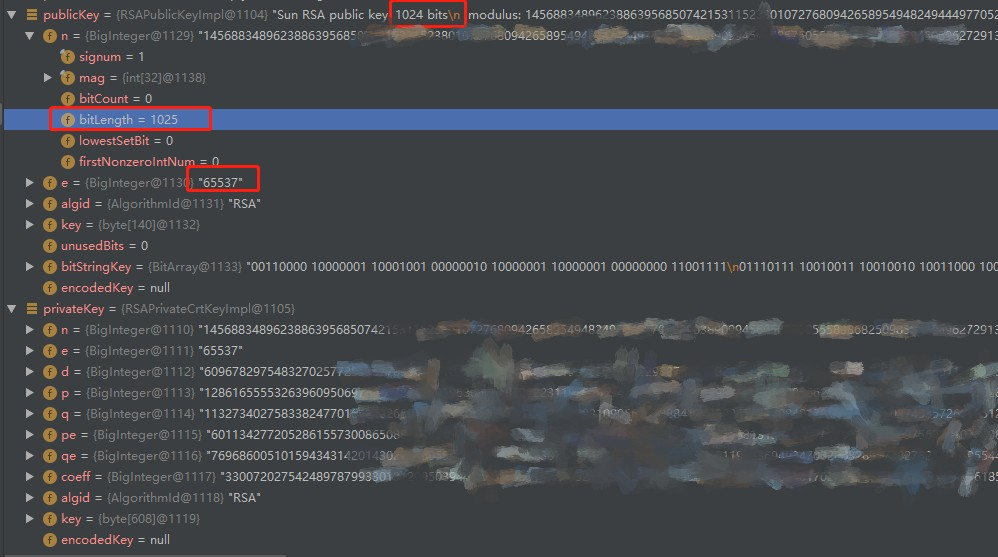
下图是从 Java keystore 文件中读取的一对 RSA Public Key, RSA Rrivate Key 的内存调试图。可以看到 n 的长度 为 1024 bit 位, publicKey 和 privateKey 的 n 的数值都相等，并且公钥 e=65537 也相等， 因此从数学上我们也可以断定publicKey 和 privateKey确实一对公私钥。注意 e=65537 不是偶然的，我测试了好几次，直接使用 KeyPair 类随机生成一对RSA 公私钥, e 也是 65537 。 从上面的数学推导过程来看，e 选择固定 65537 也是没有问题的。$65537=2^{16}+1$, 并且也是一个素数。事实上65537 是一个精心挑选的数，限于篇幅，这里不展开。