问题1:证明对任意一个闭曲线,总存在一条直线把它分成面积相等的两份。
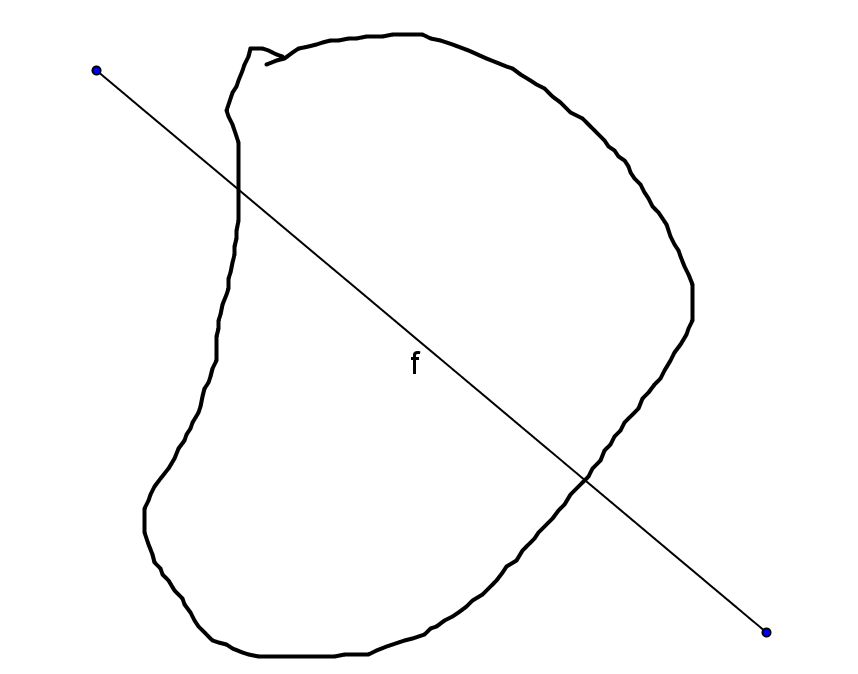
图1
零点定理介绍:若函数f(x)在区间[a,b]连续,并且f(a)与f(b)异号,那在(a,b)之间一定存在某个x,使得f(x)=0。这个定理很直观,从图像上来看,f(x)曲线肯定是要穿过x 坐标轴的。
考虑一条直线从左至右扫过整个闭曲线。刚开始左侧面积为0,右侧面积为整个面积,左侧逐渐增大为整个面积,右侧面积逐渐减小为0,这个面积变化是连续的,所以必定存在某一时刻平分整个面积,而且唯一,即角度固定时,存在唯一平分直线。
问题2:对任意一个闭曲线,是否总是存在相互垂直的两直线4等分闭曲线围成的面积?
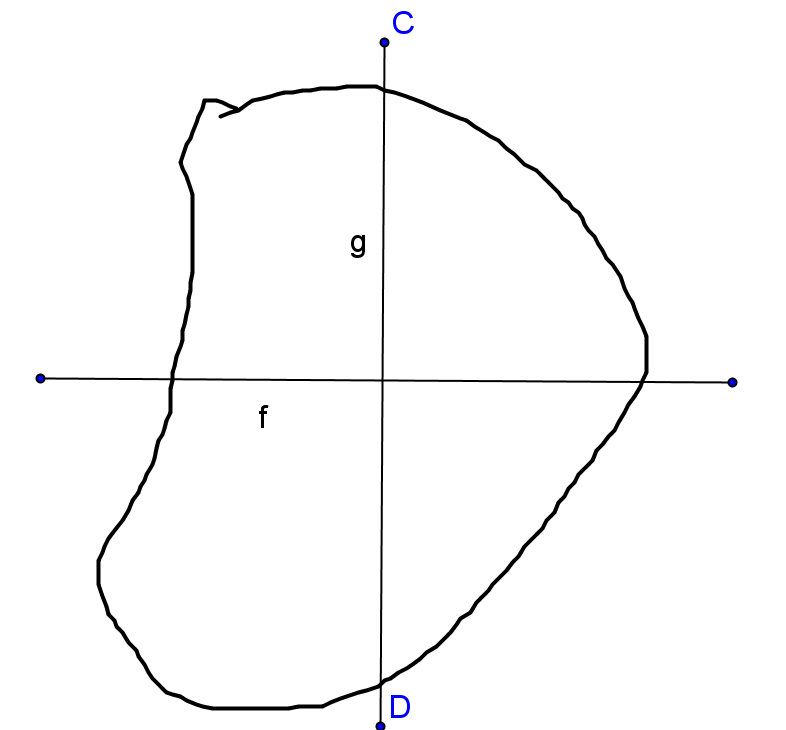
图2
我一开始的想法是,先取一条直线平分面积,另外一条垂直直线平分面积(下图的两条实线),形成4块面积。容易证明对角面积必相等,相邻面积如果相等就不需要讨论了,假设相邻面积不相等,不妨分别设面积为X, Y。 然后绕两直线的交点旋转90度,在这个过程中是连续的, 面积变化为 X->Y->X->Y , 根据零点定理会在旋转到某个角度时相等。这个证明有问题吗?
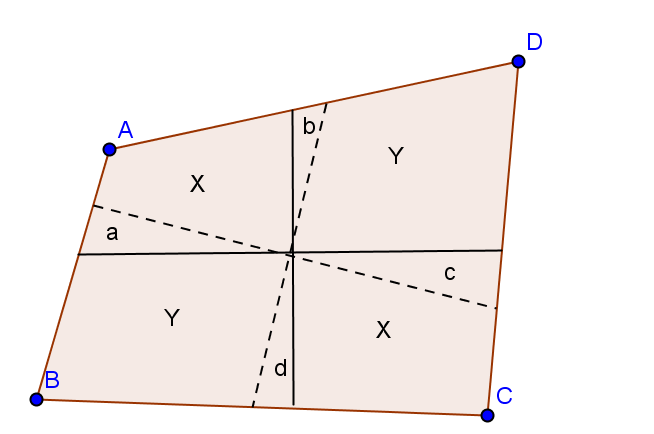
图3
表面上看上去好像问题已经解决了。但是我知道这还不足以证明。因为无法保证旋转的过程中,X+Y=S/2 (S 为总面积)。即可能旋转到某个角度时,左上角X面积刚好1/4 的面积,但是a 和 c 面积不相等 , b 和 d 面积不相等,导致其他块的面积可能或大或小。除非图形是对称的,否则这个证明有问题!
改进下,旋转的时候,允许交点做平移变换。这样可以做到在任意变换的过程中 X+Y的面积总是为S/2。但是新问题又冒出来了,在平移和旋转变换的过程中分割面积的变化仍然是连续的吗?
如下图,AB, CD 分别是平分闭曲线面积的直线, 分别旋转 θ 角度后为 EF, HG。证明前后分割面积的变化是连续的。
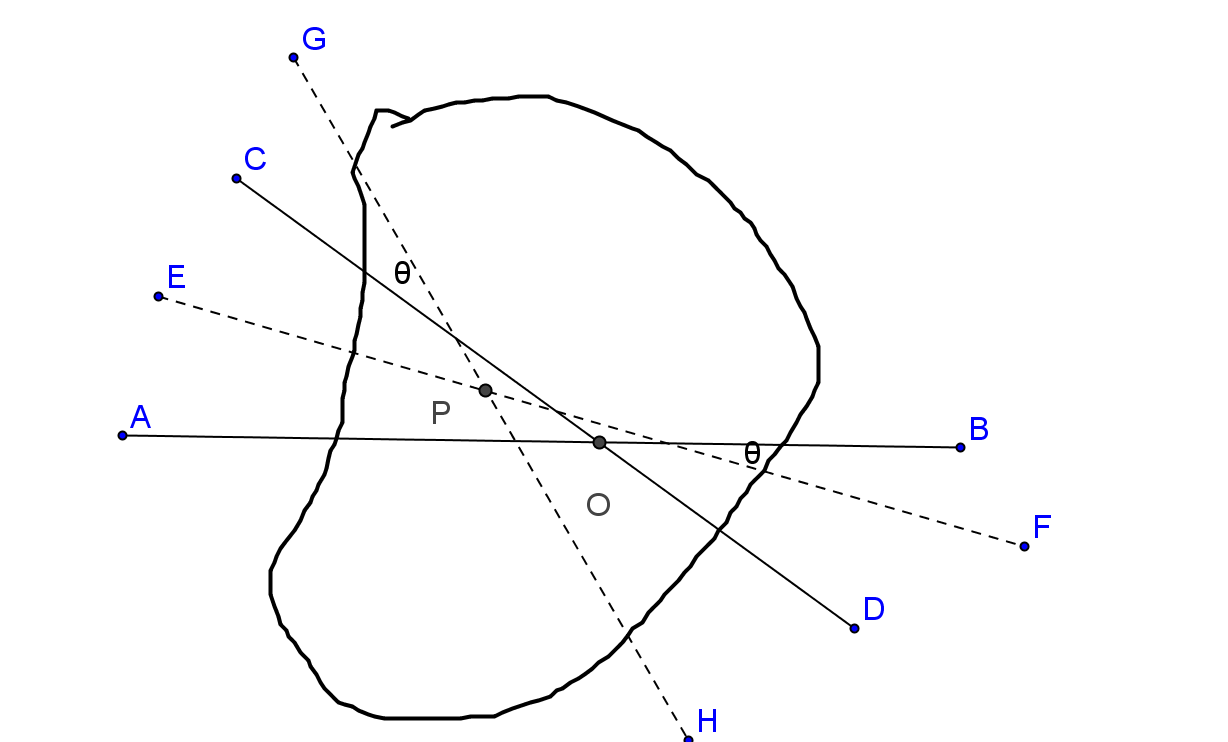
图4
证明过程:
设直线f 平分下面闭曲线面积,旋转 θ 后为g 直线,且g 直线也平分面积。那么g直线不可能和直线f相交于闭曲线外部,因为如果和直线f相交于闭曲线外部(如下图)两个面积肯定一大一小,矛盾。
注意之所以要排出这种情况是因为, 当θ 趋于0时,两直线和曲线围成的面积不一定趋于0(下图EFGH面积),面积可能会大于某个固定值(这是因为有可能两直线和曲线相交的线段EF 大于某个长度)。
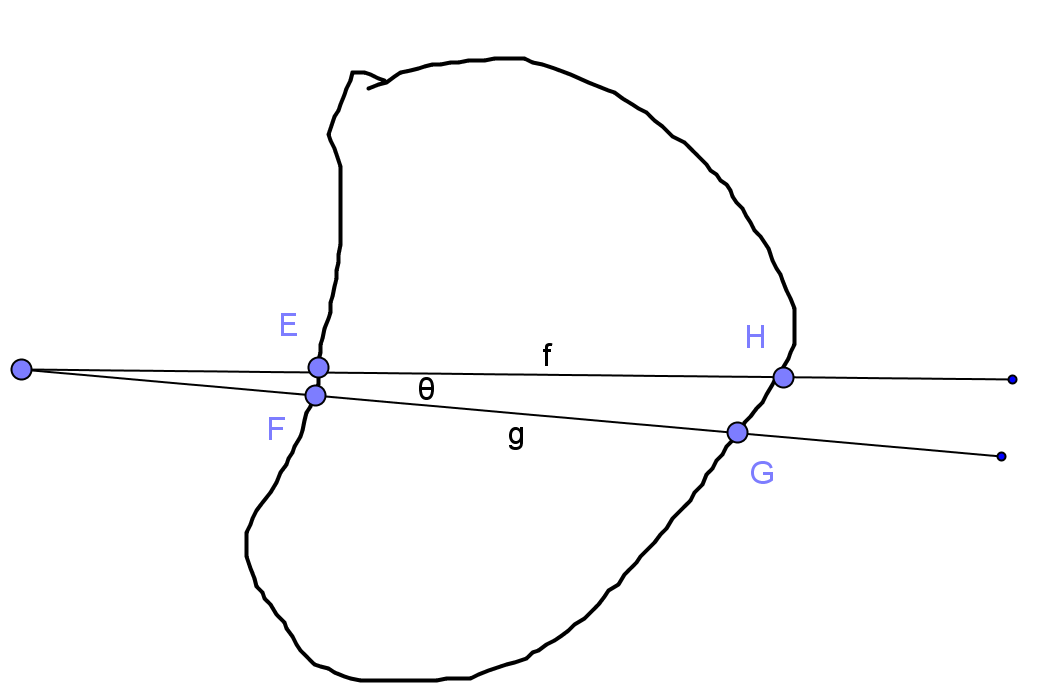
图5
所以g必定和f相交于闭曲线内部,如下图。当θ 趋于0时,两直线和曲线围成的面积也趋于0(下图OEF 和 OGH 面积)。这样图4 两直线 AB, CD 分别旋转 θ 角度后, 分割的面积变化就是这里OEF 和 OGH 面积的加加减减,所以也是趋于0的,即连续。
证毕。
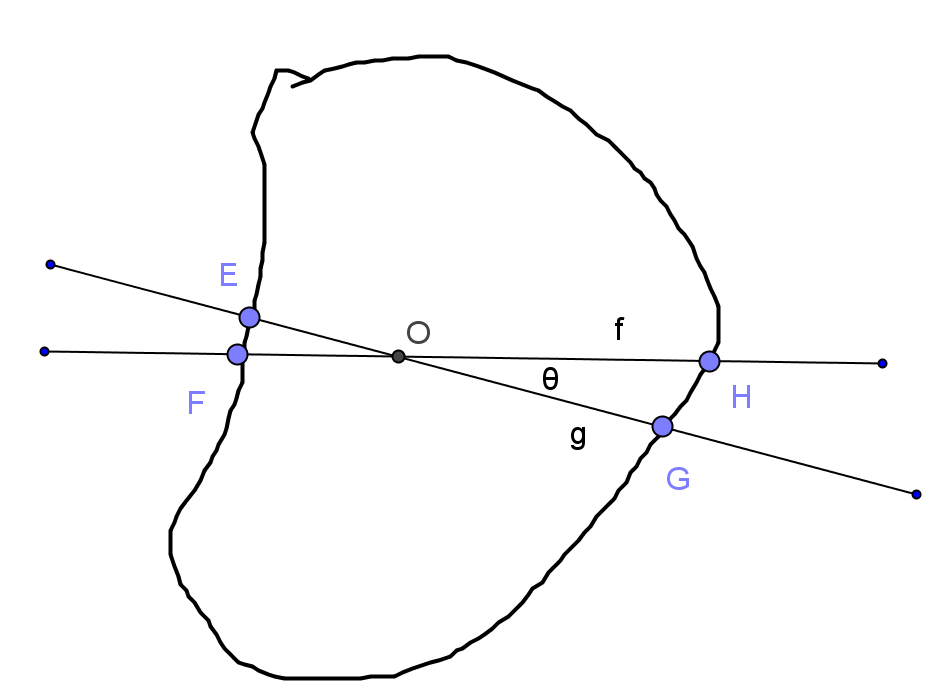
图6
