上一篇 球面两点最短距离 证明了球面两点最短距离是和球心形成的大圆的劣弧。我们利用这一结论,可以用于计算地球上两地间的最短距离。我们可以把地球看作一个标准的球体,两地间没有障碍物,不会高低不平,这样看来就特别适用于航海。而在陆地上我们可以做为一个参考距离。
我简单描述下经度和纬度的定义。在下面的球坐标系中,坐标原点为球心,z 轴为地球的自转轴,x,y 平面为地球赤道平面。x轴逆时针方向为东经方向,顺时针方向为西经方向,$\theta$ 为经度大小。线段 p 和 z 轴的夹角为 $\phi$ ,当我们说北纬几度时,等于$90-\phi$。
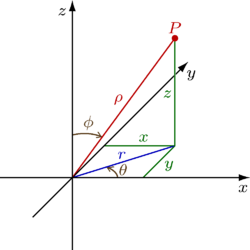
从上图根据三角正弦余弦很容易推出,直角坐标系和球坐标系的关系
$x=\rho sin\phi cos\theta$
$y=\rho sin\phi sin\theta$
$z=\rho cos\phi$
如下图, 求 B 到 C 的球面距离。分析:只要能求出角BOC 的大小,就可以求出 BC 的弧长。可以先求出 BC 的长度,然后根据正弦定理就可以求出角BAC 的大小, 而角BOC等于角BAC的2倍(圆心角为圆周角的2倍定理,从角OBA=角OAB很容易推出结论)。
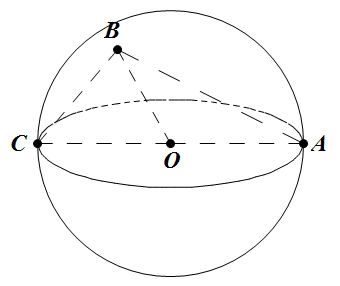
有些小伙伴可能忘记正弦定理,这里简单描述下,为了不影响本文的篇幅,证明我就不给出了:在一个三角形中,各边和它所对角的正弦的比相等, 大小为2R, R是此三角形外接圆的半径。
$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$
设半径为 R, BC线段长度为 a
$a=R\sqrt{(sin\phi_2 cos\theta_2 - sin\phi_1 cos\theta_1)^2+(sin\phi_2 sin\theta_2 - sin\phi_1 sin\theta_1)^2 + (cos\phi_2 - cos\phi_1)^2}$
$\frac{a}{sin{\angle BAC}}=2R$
$sin{\angle BAC}=\frac{a}{2R}$
由于$\angle BAC \in [0,\frac{\pi}{2}]$
而$arcsin \in [-\frac{\pi}{2}, \frac{\pi}{2}]$, 所以有
$\angle BAC=arcsin{\frac{a}{2R}}$
所以劣弧BC的长度为$2\pi R \times \frac{2\angle BAC}{2\pi}$ 即 $2R\angle BAC$
代入$\angle BAC$, 最后得到:
$2R\arcsin{\frac{\sqrt{(sin\phi_2 cos\theta_2 - sin\phi_1 cos\theta_1)^2+(sin\phi_2 sin\theta_2 - sin\phi_1 sin\theta_1)^2 + (cos\phi_2 - cos\phi_1)^2}}{2}}$
为了更加有趣好玩些,我写了一个程序接口:根据两地的经度纬度参数,计算它们的最短球面距离。考虑到大部分程序猿或多或少接触过 java ,即使没有也能猜出语句大概的意思,所以就用 java 编写。简单测试,我挑选了福州火车北站到厦门火车北站两个地点。福州北 (北纬N26°07′15.96″ 东经E119°19′30.27″)到厦门北(北纬N24°38′38.09″ 东经E118°04′57.23″)计算得出的最短球面距离为 206.3 公里,比百度地图查询得到的距离 242.8公里,大约少 36.5 公里。由于百度地图给出的是高速路线,中间有些小弯绕,再考虑到海拔的影响,多出 36.5 公里符合我的预期。如果用于计算海上的距离那会更加准确,更加符合实际的情况,所以我觉得还是有实际使用价值的。
package com.math345.algo;
/**
*
* @author yinfeng
* 可以参考我的博客文章《通过经度纬度计算两地距离》。博客地址:
* http://www.math345.com/blog/article/8
*/
public class Distance {
// 地球半径长度 单位米
public static final double EARTH_RADIUS = 6371393;
/**
* 把纬度转成球坐标和 z 轴的夹角
* @param degree >= 0 代表北纬, < 0 南纬
* @return 球坐标和 z 轴的夹角
*/
public static double convertLatitude(double degree){
return degree >= 0 ? 90 - degree : 90 - degree;
}
/**
* 把普通的度数转换成弧度
* @param degree
* @return 转换后的弧度
*/
public static double convertDegree(double degree){
return degree * Math.PI / 180;
}
/**
* 通过经度纬度计算两地距离. 其中纬度 >= 0 代表北纬, < 0 南纬
* 经度 >= 0 表示东经, < 0 表示西经
* @param latitude1
* @param longitude1
* @param latitude2
* @param longitude2
* @return 两地距离,单位米
*/
public static long calcDistanceOnEarth(double latitude1, double longitude1,
double latitude2, double longitude2){
latitude1 = Distance.convertLatitude(latitude1);
latitude2 = Distance.convertLatitude(latitude2);
return Distance.calcDistanceOnEarthByDegree(latitude1, longitude1, latitude2, longitude2);
}
/**
* 通过球坐标计算两地距离
* @param zdegree1 球坐标和 z 轴的夹角
* @param xdegree1 球坐标和 x 轴的夹角
* @param zdegree2 球坐标和 z 轴的夹角
* @param xdegree2 球坐标和 x 轴的夹角
* @return 两地距离,单位米
*/
public static long calcDistanceOnEarthByDegree(double zdegree1, double xdegree1,
double zdegree2, double xdegree2){
double x1 = convertDegree(xdegree1);
double z1 = convertDegree(zdegree1);
double x2 = convertDegree(xdegree2);
double z2 = convertDegree(zdegree2);
double a = Math.sqrt(Math.pow(Math.sin(z1)*Math.cos(x1) - Math.sin(z2)*Math.cos(x2), 2) +
Math.pow(Math.sin(z1)*Math.sin(x1) - Math.sin(z2)*Math.sin(x2), 2) +
Math.pow(Math.cos(z1) - Math.cos(z2), 2));
return Math.round(2*EARTH_RADIUS*Math.asin(a/2));
}
public static void main(String[] args) {
// 通过网址 http://www.gpsspg.com/maps.htm 查询到下面两个地点的纬度,经度
// 福州北站 26.1211,119.325074 北纬N26°07′15.96″ 东经E119°19′30.27″
// 厦门北站 24.643915,118.082565 北纬N24°38′38.09″ 东经E118°04′57.23″
// 通过百度地图,查询出福州北站到厦门北站的距离为(走的路线是高速,中间有些小弯绕 ): 242.8公里
// 比我们计算出的最短路径 206312 多36公里。
long meters = calcDistanceOnEarth(26.1211, 119.325074, 24.643915, 118.082565);
// 输出: 206312
System.out.println(meters);
}
}
您可以随意使用我的代码,但是为了尊重他人的劳动成果,请保留作者和出处,谢谢!
如果您觉得不错,请不要吝啬您的点赞,有您的支持,我才能有更大的热情写出更多的文章。
如果您觉得哪里有问题,可以评论留言,我有空都会回复。
