早上一老同学微信发我今年福建的中考数学题。上午没时间，女儿中午要吃汉堡烤鸡，店里借了笔，在餐巾纸中写了下。其实没什么难度，而且第二小题，还可以进一步缩小已知条件。发到朋友圈后，有同事建议我发给ChatGPT做，测试看看。

已知，实数 a, b, c, m, n 均满足 $3m+n=\frac{b}{a}, mn=\frac{c}{a},$

(1)求证: $b^2 - 12ac \ge 0$

(2)若a,b,c均为奇数，m,n是否有可能都是整数，请说明理由。

我的证明：

我本来是想这么简单的题，ChatGPT 应该没有问题，因此第1个就发给了 ChatGPT-4o，但是ChatGPT-4o 的回答惨不忍睹。第一小题，确实也可以使用韦达定理的逆定理解决，ChatGPT-4o 就想使用该方法，可惜它系数构造错了，说系数要调整，然后直接跳到结论 $b^2 - 12ac$ 大于等于0。 其实系数的构造很简单，设两根为$x_1=3m, x_2=n$，则$x_1x_2=3mn=\frac{3c}{a}$，因此 3m, n 是下面二次方程的2个根

\[ax^2 -bx + 3c = 0,\]

判别式$b^2-12ac$ 必定大于等于0。第二小题简直是胡言乱语。

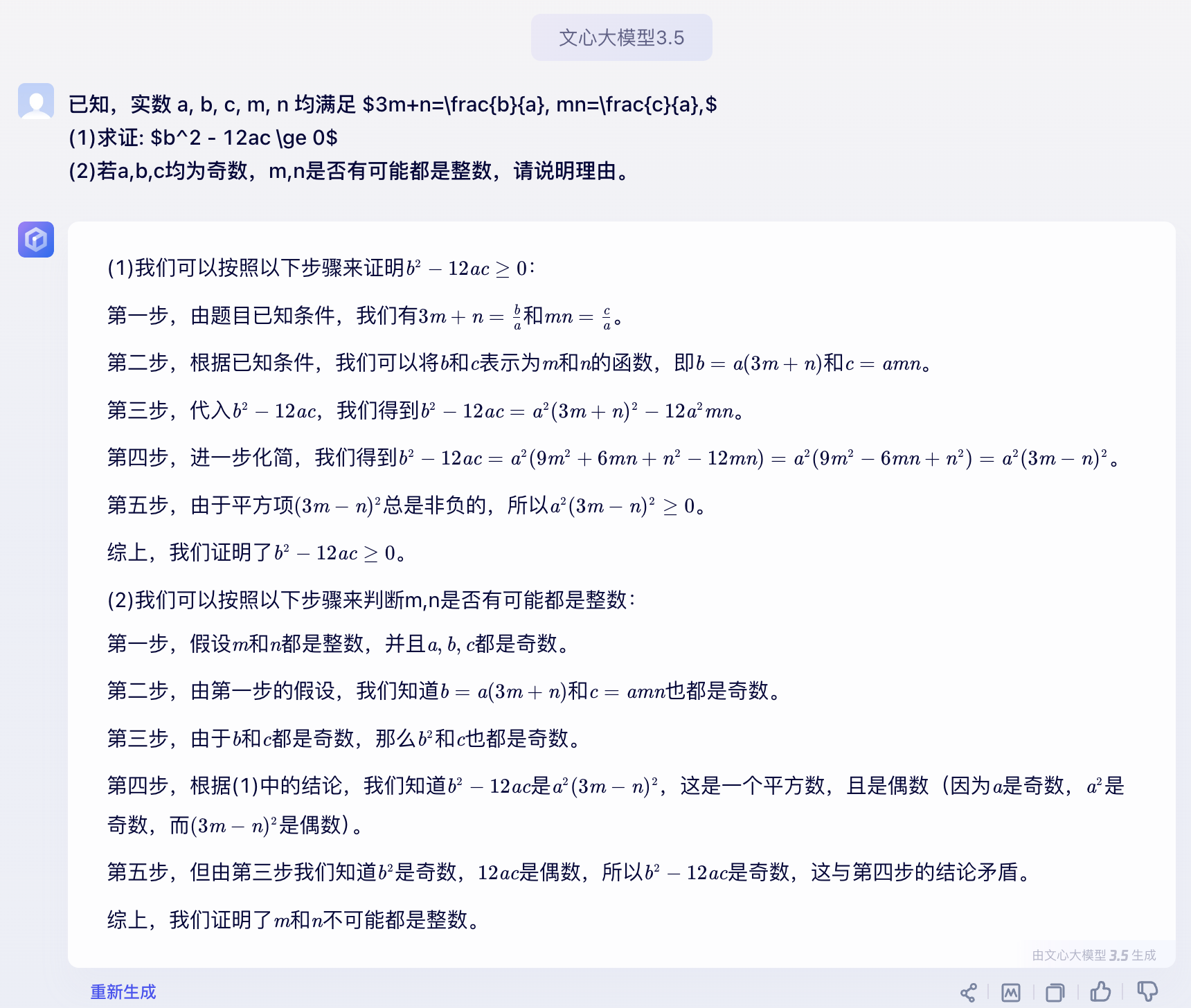
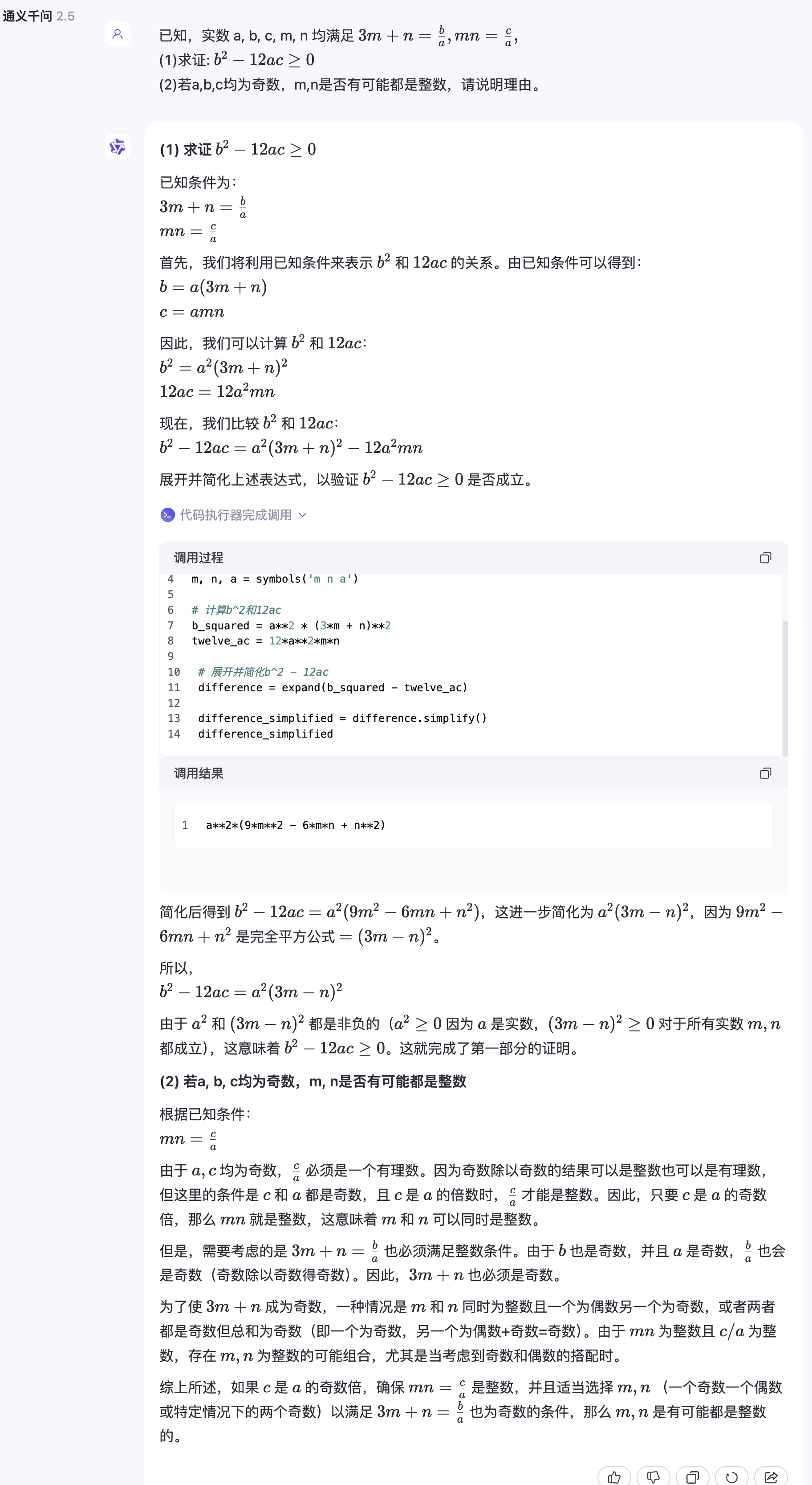
我猜测ChatGPT-4o由于是个多模态模型（支持语言、语音、图像、视频）导致了它在数学方面的减弱。 于是我发给阿里的的通义千问2.5模型看看，通义千问第一小题正确，第二小题错误。最后我发给百度的文心大模型3.5，文心3.5第一小题正确，第二小题可以得一半的分，因为它没有说清楚为什么 $(3m-n)^2$ 是偶数，应该先推出 m 和 n 都是奇数，才可以得出这个结论。

注意到文心第二小题的证明利用了第一小题计算结论，$b^2-12ac=a^2(3m-n)^2$ ，其实用这个结论显然增加了复杂度，我的证明就没有使用，直接用已知条件就足够了。

大模型的回答请参考下面的截图。

从这里我们也可以对当前大模型的能力有个基本认识：数学其实也是一门语言，有自己独特的符号，强调逻辑、推理以及计算，但数学又不像编程语言一样那么严密 -- 因为数学的表达基本还是靠自然语言和数学符号组织构成的。因此大模型可以解决一些数学问题，毕竟它已经学过海量的数学题（题海战术），它可以像人类做梦那样不加思索地照搬学过的解题套路解决问题。如果这个套路刚好正中下怀，那么就可以轻松解决（如第一小题）；如果这个套路错了，那么模型无法意识到已经错了要尝试换个套路尝试，它会非常有勇气并信心满满地继续自圆其说。简单的说当前的大模型缺乏自省能力！如果大模型加上了自省能力，那将非常可怕，达到人类甚至超过人类的智能将不在话下。

用孔子说的话评大模型最好不过了：知之为知之，不知为不知，是知也。

话说回来，即使当前的大语言模型有幻觉（缺乏自省能力）对数学教育、数学研究也是非常有益的，毕竟它可以给我们一些思路或灵感。在编程领域就更不用说了。