如果一个随机变量具有概率密度函数
\begin{align*} f(x)=\frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty \end{align*}
则称X为正态随机变量并记为$X \sim N(\mu, \sigma^2)$.这里N 为“Normal” 一词的首字母.$\mu, \sigma$ 都是常数,$\mu$ 为均值,可以取任何实数值, 而$0 < \sigma^2 < \infty$ 为方差,$\sigma$ 称为标准差。这种分布我们称之为正态分布,德国数学家Gauss率先将其应用于天文学研究,故正态分布又叫高斯分布。
下面是$\mu=1, \sigma=1$ 和 $\mu=1,\sigma=\frac{1}{2}$ 的正态分布概率密度函数图像:
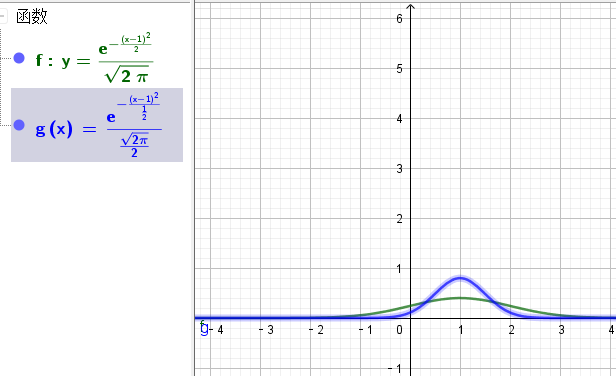
我们知道 $x=\mu$ 均值时,概率密度值最大,比如当标准差 $\sigma=1$ 时的概率密度值为
\[f(\mu) = \frac{1}{\sqrt{2\pi} \sigma} = 0.3989\]
问题1: t个标准差范围内的概率 $P(u-t\sigma \le x \le u+t\sigma)$ 是一个定值吗?和参数$u, \sigma$ 有没有关系? 其中 t 为大于0的实数。
下图在很多关于概率的书本中都可以找到,它形象的展示了正态分布下,值离均值的距离为-1个标准差到1个标准差的概率约为68\%(即曲线从-1到1围成的面积),-2个标准差时概率约为95\%,-3个标准差时概率约为99.7\% 。但是大部分教材没有告诉我们为什么就是一个定值,这个值是怎么计算出来的?
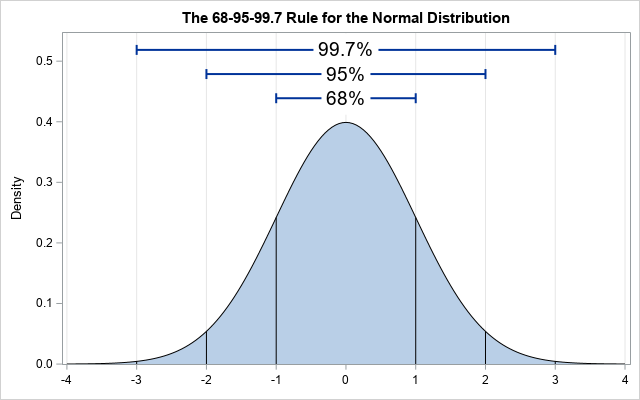
其实我们做下下面的变换,就可以断定:不论是什么参数下的正态分布,t个标准差范围内的概率$P(u-t\sigma \le x \le u+t\sigma)$都是一个定值,和参数$u, \sigma$ 无关,这真是一件神奇的事情。
\begin{align*} &P(u-t\sigma \le x \le u+t\sigma) \\ &= \int_{u-t\sigma}^{u+t\sigma} \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx \\ &= \frac{1}{\sqrt{2\pi} \sigma} \int_{u-t\sigma}^{u+t\sigma} e^{-(\frac{x-\mu}{\sqrt{2}\sigma})^2} dx \\ &=\frac{\sqrt{2}\sigma}{\sqrt{2\pi} \sigma} \int_{u-t\sigma}^{u+t\sigma} e^{-(\frac{x-\mu}{\sqrt{2}\sigma})^2} d\frac{x-\mu}{\sqrt{2}\sigma} \\ &=\frac{2}{\sqrt{\pi}} \int_{0}^{\frac{t}{\sqrt{2}}} e^{-y^2} d y \qquad (1) \end{align*}
问题2:如何计算(1)式 ?
如果我们直接去求不定积分 $\int e^{-x^2} dx$ 的初等函数表达式,那我们就会掉进坑里。因为$e^{-x^2}$这个函数的原函数不是初等函数!
为了解决上面的问题,这里先介绍下$e^{-x^2-y^2}$函数的二重积分,转成极坐标的形式计算。下面面积D是一个半径$\rho=a$的圆。
\begin{align*} \int\int_D e^{-x^2-y^2} dx dy &= \int_0^{2\pi} \int_0^a e^{-\rho^2} \rho d\rho d\theta \\ &= \int_0^{2\pi} -\frac{1}{2}e^{-\rho^2}\Big|_0^a d\theta \\ &= \int_0^{2\pi} -\frac{1}{2}(e^{-a^2} -1) d\theta \\ &= \frac{1}{2}(1-e^{-a^2})\theta \Big|_0^{2\pi}\\ &= \pi(1-e^{-a^2}) \qquad (2) \end{align*}
不难想象这个函数的图形,首先考虑一元函数 $e^{-x}$ 的图形,然后注意到 $-(x^2+y^2) \le 0$, 即$e^{-(x^2+y^2)}$的最大值为$e^0=1$, 其次 $x^2+y^2$ 可以看成半径从 0 到 $+\infty$ 变化的圆, 半径越大 $e^{-(x^2+y^2)}$ 越小,所以它的图像应该长下面的样子:
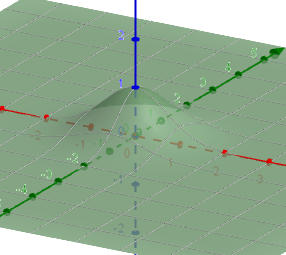
那么如何建立起 $\int_0^{+\infty} e^{-x^2} dx$ 和 $\int\int_D e^{-x^2-y^2} dx dy$ 的关系?不难想到
\[ \int_0^{+\infty} e^{-y^2} dy = \int_0^{+\infty} e^{-x^2} dx \]
那么
\begin{align*} (\int_0^{+\infty} e^{-x^2} dx )^2 &= \int_0^{+\infty} e^{-x^2} dx \int_0^{+\infty} e^{-y^2} dy \\ &= \int_0^{+\infty} \int_0^{+\infty} e^{-x^2-y^2} dx dy \\ &= \frac{1}{4} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-x^2-y^2} dx dy \\ &=\frac{1}{4}\lim_{a \to \infty} \pi(1-e^{-a^2}) \\ &=\frac{\pi}{4} \end{align*}
于是得到
\[\int_0^{+\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2} \qquad (3)\]
但是上面计算的是0到无穷的积分,(1)式中我们要计算的是0到某个固定值的积分。具体的讲,我们要求的积分区域如下图,正方形 S 是 $\int_0^{R} \int_0^{R} e^{-x^2-y^2} dy dx$ 的积分区域, $\int\int_D e^{-x^2-y^2} dx dy = \pi(1-e^{-a^2})$ 中的 D 是由中心在原点、半径为 a 的圆周所围成的闭区域, 下图中 $D_1,D_2$ 是 $a=R, a=\sqrt{2}R$ 时相应 D 区域的 $\frac{1}{4}$。
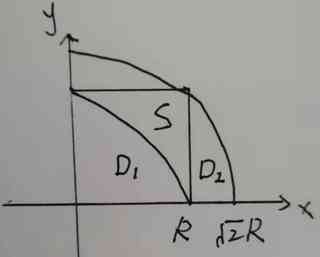
因此
\begin{align*} \int\int_{D_1} e^{-x^2-y^2} dx dy < \int\int_S e^{-x^2-y^2} dx dy < \int\int_{D_2} e^{-x^2-y^2} dx dy \end{align*}
于是上面的不等式可以写成
\[\frac{\pi}{4}(1-e^{-R^2}) < (\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-2R^2}) \qquad (4)\]
但是上面这个不等式比较粗糙,我们可以构造更加精确的上下界。
对于上界,我们可以找到1/4圆面积恰好等于正方形$R^2$的面积,如下图

此时圆的半径$r_1$为
\[\frac{\pi r_1^2}{4} = R^2 \Rightarrow r_1^2 = \frac{4R^2}{\pi}\]
由于$e^{-x^2-y^2}$是单调递减函数,因此必定有此上界:
\[(\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-4R^2/\pi}) \qquad (5)\]
对于下界,如下图,我们可以找到
\[r_2 \text{到} \sqrt{2}R \text{的阴影面积}S_1 = \text{正方形面积} S-D_1\]
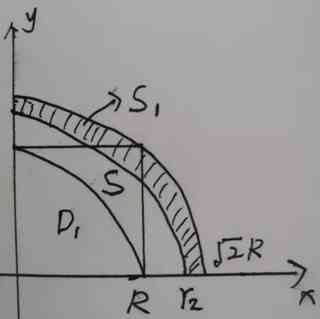
由于$e^{-x^2-y^2}$是单调递减函数,因此有
\[(\int_0^R e^{-x^2} dx)^2 > \int_{D_1+S_1} e^{-x^2-y^2} dx dy\]
此时圆的半径$r_2$为
\begin{align*} &R^2-\frac{\pi R^2}{4} = \frac{2\pi R^2}{4} - \frac{\pi r_2^2}{4} \\ \Rightarrow &r_2^2 = 3R^2 - \frac{4}{\pi}R^2 \end{align*}
因此必定有此下界:
\begin{align*} (\int_0^R e^{-x^2} dx)^2 &> \frac{\pi}{4}(1-e^{-R^2}) + \frac{\pi}{4}(1-e^{-2R^2}) - \frac{\pi}{4}(1 - e^{-3R^2 + \frac{4}{\pi}R^2}) \\ &> \frac{\pi}{4}(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2}) \qquad (6) \end{align*}
合并(5)(6)式,得到了比(4)式更加精确的不等式(7)
\begin{align*} \frac{\pi}{4}(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2}) <& (\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-4R^2/\pi}) \qquad (7)\\ \frac{\sqrt{\pi}}{2}\sqrt{(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2})} <& \int_0^R e^{-x^2} dx < \frac{\sqrt{\pi}}{2}\sqrt{1-e^{-4R^2/\pi}} \qquad (8) \end{align*}
回到(1)式
\begin{align*} P(u-t\sigma \le x \le u+t\sigma) =\frac{2}{\sqrt{\pi}} \int_{0}^{\frac{t}{\sqrt{2}}} e^{-x^2} d x \end{align*}
在不等式(8)中,取 $R=\frac{t}{\sqrt{2}}$ , 得
\begin{align*} \sqrt{1-e^{-t^2/2} - e^{-t^2} + e^{-3t^2/2 + 2t^2/\pi}} < P(u-t\sigma \le x \le u+t\sigma) < \sqrt{1-e^{-2t^2/\pi}} \qquad (9) \end{align*}
于是写个python程序计算下
def normal_prop_lowerbound(t): return math.sqrt(1-math.exp(-t*t/2)-math.exp(-t*t)+math.exp(-1.5*t*t+2/math.pi * t*t)) def normal_prop_upperbound(t): return math.sqrt(1-math.exp(-2*t*t/math.pi)) if __name__ == '__main__': print(normal_prop_lowerbound(1), "< 均值为中心1个标准差范围内的概率 <", normal_prop_upperbound(1)) print(normal_prop_lowerbound(2), "< 均值为中心2个标准差范围内的概率 <", normal_prop_upperbound(2)) print(normal_prop_lowerbound(3), "< 均值为中心3个标准差范围内的概率 <", normal_prop_upperbound(3))
程序输出:
0.6688228555159094 < 均值为中心1个标准差范围内的概率 < 0.6862377078915619
0.9370075438591285 < 均值为中心2个标准差范围内的概率 < 0.9600223595773711
0.9945801268713956 < 均值为中心3个标准差范围内的概率 < 0.998374454827675
另外,注意到,在(9)不等式中,当我们令 R 趋于正无穷,上式两端同时趋于极限1, 从而我们也验证了正态分布的概率密度函数的积分即概率确实为1. 当然在比较粗糙的(4)不等式中,令 R 趋于正无穷,也可以验证了正态分布的概率密度函数的积分即概率确实为1.
应用场景一: 有一堆数据我们想知道是否服从正态分布,我们可以通过统计1、2、3个标准差范围内的数据的概率是否大致符合0.68,0.95,0.997的概率来校验。如果不太符合这些概率,那么就不太可能是正态分布。
应用场景二: 有一堆数据假设服从正态分布,我们想知道那些数据是异常的,那么我们就可以设定t个标准差范围内的数据是正常的,即超过t个标准差的数据即$|x-u| > t\sigma$是异常的,取t为多少是合适的,就看我们的应用场景下的异常数据的概率有多大。
