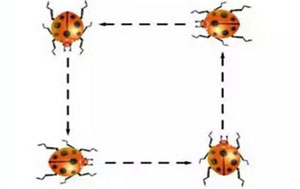
美国天文学家、纽约海登天文馆“老总”泰森在自传中提到自己小时候（11岁时）最喜欢的一道智力题是这样的：四只虫子在一个边长一英尺的正方形的四个角上，同时开始以相同的速度追自己前方的虫子 （即方向始终对准前方虫子），问追上时每只虫子爬了多少路？您不妨先想想，然后再看答案。
有些同学认为虫子总是在正方形边上，速度相等永远追不上，误解了题意。我画了草图，如下，即虫子的路线看上去应该是条螺线。
上一篇 球面两点最短距离 证明了球面两点最短距离是和球心形成的大圆的劣弧。我们利用这一结论，可以用于计算地球上两地间的最短距离。我们可以把地球看作一个标准的球体，两地间没有障碍物，不会高低不平，这样看来就特别适用于航海。而在陆地上我们可以做为一个参考距离。
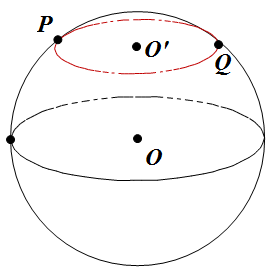
平面上两点最短距离大家都知道直线最短，这是公理，因为这连牛都知道（小牛肯定优先选择直线跑向牛妈）。但是球面两点最短距离就不是凭直觉可以知道的了。 比如下图 P、Q 两点的最短距离是大圆 O 上的劣弧，还是小圆 O'上的劣弧，还是其它弧呢？注：劣弧指的是两段弧中较短的弧。
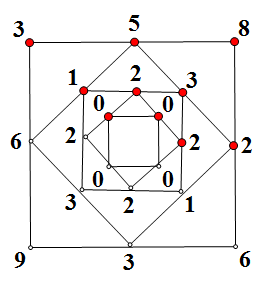
一个正方形，作出它的中点正方形；再作出新正方形的中点正方形，依次类推，会生成一个漂亮的图案。
如果在原正方形的四个顶点处随意各写1个自然数，将相邻顶点处数字相减（用较大数减较小数），结果写在每条边的中点（若数字相等，记为0）；依此类推，发现：不管当初写下的数字如何，最后得到的四个数字都是0。
例如下图：
要证明，确有些难度。
在维基百科是这样介绍芝诺悖论的：
芝诺悖论是古希腊数学家芝诺（Zeno of Elea）（盛年约在公元前464-前461）提出的一系列关于运动的不可分性的哲学悖论。这些悖论由于被记录在亚里士多德的《物理学》一书中而为后人所知。芝诺提出这些悖论是为了支持他老师巴门尼德关于“存在”不动、是一的学说。这些悖论是芝诺反对存在运动的论证其中最著名的两个是：“阿基里斯追乌龟”和“飞矢不动”。
下面是我之前的笔记，整理如下。
某次会议一共有100个人参加，其中某些人之间握过手，但每两个人之间最多只会握一次手。会议结束后，不同的人握手的次数不同，有的人握手次数少，有些人握数次数多。问：是否一定能找到两个人，他们握手的次数是相同的？您不妨先自己思考几分钟，然后再阅读。
