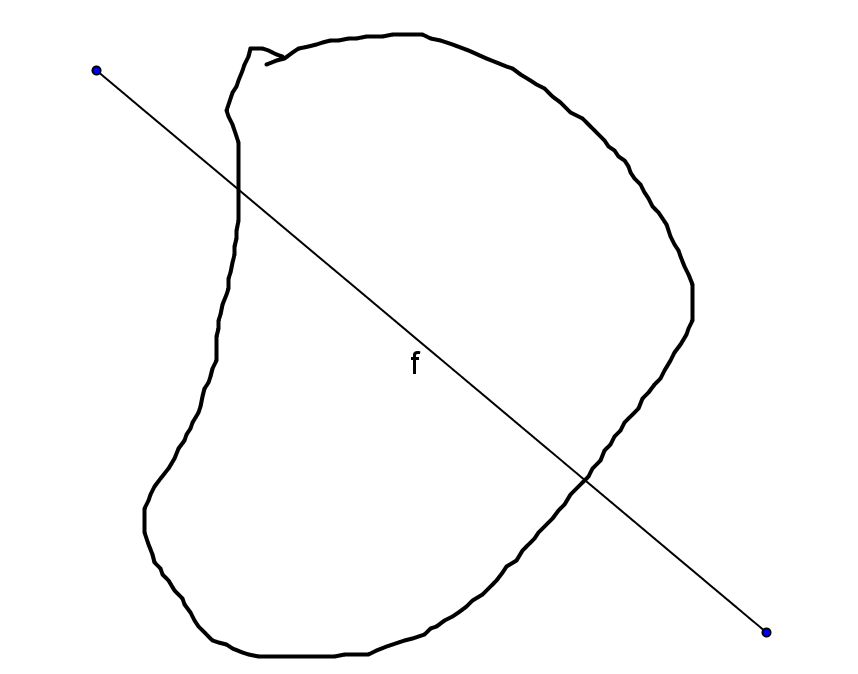
一个点在x 轴行走,起始点在原点,每次走 1 格,每次的方向随机或正或负,概率均为1/2。行走 n 步后,预期该点相对原点的绝对距离是多少呢?
poolDequeue 的 eface 和 dequeueNil
golang 中的 poolDequeue 是 ring buffer 的一种实现. ring buffer 是一种无锁循环队列。这里的 poolDequeue 仅支持1个生产者,但可以有多个消费者(通过 CAS 实现),因为无锁,所以性能非常好。ring buffer 这里不展开,网上很多资料。
这里重点通过 eface 和 dequeueNil 来阐明golang 中的 interface{} 是由 type 和 value 2个机器字组成。当 type 和 value 都为nil(即null ) 时, 才为 nil 的interface;当 type!=nil,value==nil 时,不是 nil 的interface.
与归并排序一样,快速排序也使用了分治思想。下面是对一个典型的子数组A[p..r] 进行快速排序的三步分治过程:
分解:数组A[p..r]被划分为两个(可能为空)子数组A[p..q-1]和A[q+1..r],使得A[p..q-1]中的每一个元素都小于等于A[q],而A[q]也小于等于A[q+1..r]中的每个元素。其中,计算下标q也是划分过程的一部分。
解决:通过递归调用快速排序,对子数组A[p..q-1]和A[q+1..r]进行排序。
合并:因为子数组都是原址排序的,所以不需要合并操作:数组A[p..r]已经有序。
在常见的分布式系统中,总会发生诸如机器宕机或网络异常(包括消息的延迟、丢失、重复、乱序,还有网络分区)等情况。Paxos算法需要解决的问题就是如何在一个可能发生上述异常的分布式系统中,快速且正确地在集群内部对某个数据的值达成一致,并且保证不论发生以上任何异常,都不会破坏整个系统的一致性。
证明:当概率均等时信息熵最大。即当 $p_i=\frac{1}{n}$ 时,下面的 H 取得最大值。
\[H=-\sum\limits_{i=1}^{n} p_i log {p_i}=\log n\]
一场活动要测试鸵鸟蛋的坚固性。要让蛋从高楼上落下而不破,进而依据不破的最高楼层决定蛋的硬度。测试的高楼共101层。测试员意识到,如果他只带一颗鸵鸟蛋的话,他需要从第1层开始往上依次每一层把蛋投下以判定蛋的硬度。
如果他带两颗鸵鸟蛋(假定坚固性一样),那么在最坏的情况下他需要测试多少次呢?
最近考上南京邮电大学的徐玉玉学费被骗身亡,清华教授被骗1760万,暴露了很多问题,比如银行系统/制度的漏洞,我们的身份、隐私泄漏问题。今天早上想到下面这么个问题。
小明和小白在火车上相遇,聊得很投缘。小明想知道自己的生日和小白是否相同,但是由于刚刚认识,想尽量保护双方的隐私(能满足如果生日不一样不希望对方知道自己的生日即可)。请你给他们出一个方案。