一个正方形,作出它的中点正方形;再作出新正方形的中点正方形,依次类推,会生成一个漂亮的图案。
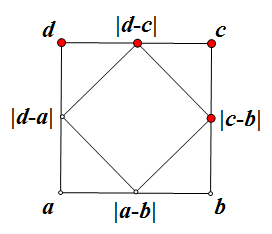
如果在原正方形的四个顶点处随意各写1个自然数,将相邻顶点处数字相减(用较大数减较小数),结果写在每条边的中点(若数字相等,记为0);依此类推,发现:不管当初写下的数字如何,最后得到的四个数字都是0。
例如下图:
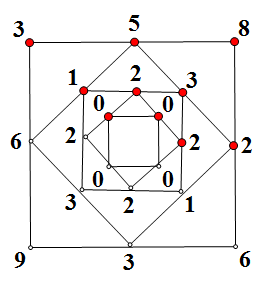
要证明,确有些难度。
首先,我注意到当其中一对角顶点相等时,如下图,必然最终4个顶点为0。
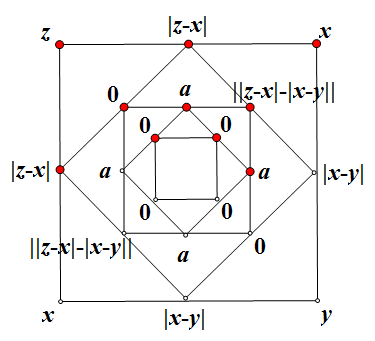
接着再研究下,其中一相邻两个顶点为0的情况。
(1)假设 y>x ,如下图,等价于上面一对角顶点相等的情况,所以最终必为0。
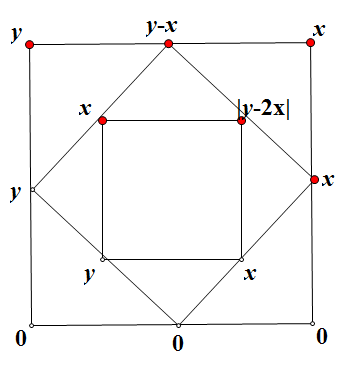
(2) 假设 y<x ,如下图,仍等价于一对角顶点相等的情况,最终必为0。
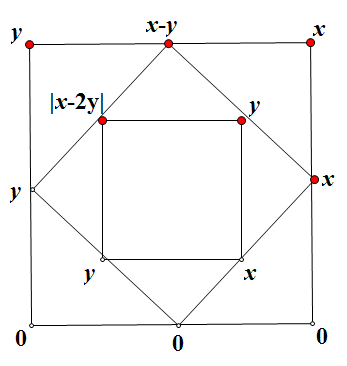
现在分析一般的情况,设4个顶点为 a,b,c,c 不全为0(否则就没讨论的必要了)。
a,b,c,d 如果有两个以上为0,那么要么相邻,要么对角,从上面的分析可知,必然最终归0。
a,b,c,d 如果都不为0,那么他们中的最大数 max{a,b,c,d} 必然比上次小。如果一直不出现0,那么 max{a,b,c,d} 必然会减小到0为止。如果出现一个0,那么转为下面第3种情况。
3. a,b,c,d 其中一个为0,不妨假设d为0(假设其它为0实质上都是一样的,因为旋转下图形就一样了)。从下图可以看到,只有当a=b>c 或 b=c>a 的情况,第3个正方形的最大顶点数和第一个正方形的最大顶点数相等,但是即便如此,第4个正方形的最大顶点数必然要减小(第4个正方形没有画出来)。所以此种情况仍然不能阻止 max{a,b,c,d}的减小。
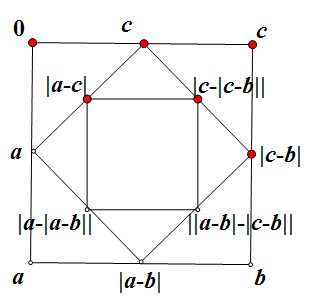
综上已经证明最后四个数字必为0。
从另一个角度来看,是因为找不到一个稳定结构,使得max{a,b,c,d}不减小。比如三角形就可以找到一个稳定结构,所以对于三角形这个命题是不成立的。例如下面的情形,三角形就可以周而复始稳定循环。
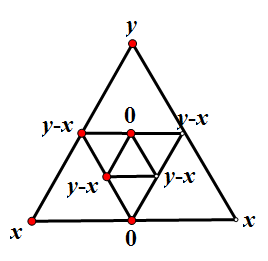
这让我想到了类似问题(通过一定运算规则,最终会变为某数的问题)中的 Collatz 猜想,也叫做 3 · n + 1 问题。这个问题是这样的:任意取一个正整数 n ,如果 n 是奇数,则把 n 变为 3 · n + 1 ;如果 n 是偶数,则把 n 变为 n/2 。不断重复操作,则最终一定会得到 1 。
举个例子,如果 n = 26 ,那么经过下面 10 步之后,它最终变为了 1 :
26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
看上去如此简单,却至今还没有人能证明它是正确的或是错误的。
