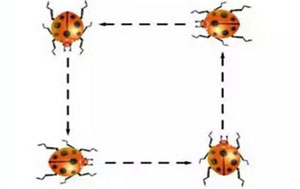
美国天文学家、纽约海登天文馆“老总”泰森在自传中提到自己小时候(11岁时)最喜欢的一道智力题是这样的:四只虫子在一个边长一英尺的正方形的四个角上,同时开始以相同的速度追自己前方的虫子 (即方向始终对准前方虫子),问追上时每只虫子爬了多少路?您不妨先想想,然后再看答案。
有些同学认为虫子总是在正方形边上,速度相等永远追不上,误解了题意。我画了草图,如下,即虫子的路线看上去应该是条螺线。
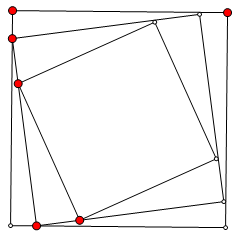
一开始,我也没有想到一个好的思路。仔细琢磨后,一副画面从我脑海呈现,相邻虫子相互牵着一条直线,又由于每只虫子始终对准前方虫子,所以直线的斜率虽然一直在变化,但是任一时刻虫子始终都是朝着直线指向的方向爬的,可以猜测虫子追上前方的虫子和它们之间的直线长度相等,即等于正方形边长1英尺。
上面只是想象和猜测。如何用数学计算或证明呢? 我使用的是数列求和的方法。过程如下:
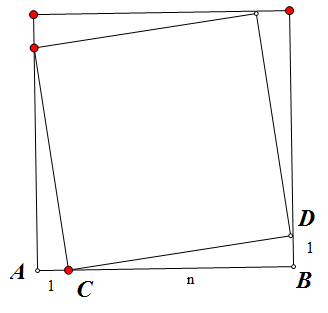
任一时刻,4只虫子形成的都是正方形,如上图,不妨把正方形边长AB 分成 1+n 份,每只虫子前进 1 份长的距离,记 AC = 1, BC = n, BD = 1 。这样从 A 到 C ,相邻虫子缩短的距离如下(AB 长度减去 CD 长度):
$n+1-\sqrt{n^2+1}$
也就是说,前进1份的长度,相邻虫子缩短的距离为 $n+1-\sqrt{n^2+1}$ 份的长度,它们的比值为
$\frac{1}{n+1-\sqrt{n^2+1}}$
注意下一时间段,下下一时间段... 这个比值始终都是是固定的。那么当相邻虫子每次缩短的距离加起来和最初的正方形边长相等时,它们就相遇了。
正方形最初长度为1英尺,设相遇时虫子爬行的总长度为 x ,总共需要缩短的距离就为1英尺,根据上面推理,下面的等式会成立:
$\frac{x}{1英尺}=\frac{1}{n+1-\sqrt{n^2+1}}$
所以x为:
$x=\frac{1}{n+1-\sqrt{n^2+1}} \times 1英尺$
根据题意,可知 n 为无穷大,所以 $n+1-\sqrt{n^2+1}$ 的极限趋于1,所以 x 趋于正方形边长,当n无穷大时,x 等于正方形边长,即每只虫子需爬行1英尺。
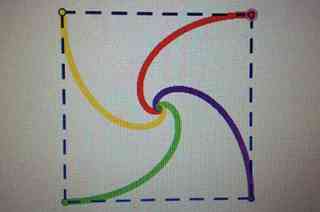
后记:网上查了一下资料,才知道这叫等角螺线。轨迹大概如下图:
参考资料:
