证明：当概率均等时信息熵最大。即当 $p_i=\frac{1}{n}$ 时，下面的 H 取得最大值。

\[H=-\sum\limits_{i=1}^{n} p_i log {p_i}=\log n\]

证明： 先证明一个结论：

两个概率变量 x,y 满足 $x+y=p, 0 < p \le 1$, p 为一定值，当 x 越靠近 $\frac{p}{2}$ 时，下面的z越大

\[z=-(x\log x+(p-x)\log (p-x))\]

对x求导

\begin{align*} z' &= -(\log x+x\frac{1}{x} - \log(p-x)-(p-x)\frac{1}{p-x}) \\ &= -\log \frac{x}{p-x} \end{align*}

当 $x=\frac{p}{2}$ 时，$z'=0$;

当 $x<\frac{p}{2}$ 时，$z'>0$; 单调递增;

当 $x>\frac{p}{2}$ 时，$z'<0$; 单调递减;

所以，$x=\frac{p}{2}$ 为最大值点，x 越靠近 $\frac{p}{2}$ 时 z 越大。

下面是 z 函数示意图, 注意这里对数是以 e 为底的，如果以 2 为底，最大值为 1 。

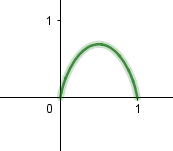
回过头来，证明命题。假设 $p=\frac{1}{n}$, 定义

\[x_1=min(p_i)<max(p_i)=x_2\]

则必有 $x_1 < p < x_2$, 由此可推出

\[-(p\log p +(x_1+x_2-p)\log (x_1+x_2-p)) > -(x_1\log x_1 + x_2\log x_2) \]

这是因为若 $p \le \frac{x_1+x_2}{2}$, 则 p 比 $x_1$ 靠近 $\frac{x_1+x_2}{2}$, 所以左式大；若$p > \frac{x_1+x_2}{2}$, 则 p 比 $x_2$ 靠近 $\frac{x_1+x_2}{2}$, 所以左式大。

每一轮我们都把最小、最大的 $p_i$ 所对应的两项 $-p_i\log p_i$ 的值变成了 $-(p\log p +(x_1+x_2-p)\log (x_1+x_2-p))$ , 并且 H 增大，$\sum_{i=1}^n p_i = 1$ 保持了概率和为1。

经过 n-1 轮后，所有的项的值都变成了 $-p\log p$， 达到最大值。 所以 $p=\frac{1}{n}$ 时H 取得最大值$\log n$。