在常见的分布式系统中，总会发生诸如机器宕机或网络异常（包括消息的延迟、丢失、重复、乱序，还有网络分区）等情况。Paxos算法需要解决的问题就是如何在一个可能发生上述异常的分布式系统中，快速且正确地在集群内部对某个数据的值达成一致，并且保证不论发生以上任何异常，都不会破坏整个系统的一致性。

在这个一致性算法中，有三个参与角色，我们分别用Proposer，Acceptor和Learner 来表示。在算法的每个实例中，每个服务器担任所有角色（Proposer，Acceptor和Learner）。

术语要定义清楚，翻译要准确一致。比如术语 chosen 和 accept 在Paxos Made Simple 论文中是通过斜体明确提示读者注意区别的。但是在在倪超的书就有些小瑕疵，没有给出选定提案和批准提案的区别，Accept 大部分是翻译成批准的，但也有的地方翻译成通过。例如 35 页:如果 Acceptor收到这个针对$[M_n,V_n]$ 提案的 Accept 请求,只要该 Acceptor 尚未对编号大于$M_n$ 的 Prepare 请求做出响应,它就可以通过这个提案。看了Paxos Made Simple 论文我才明白：一个 Acceptor 可以 Accept 通过一个提案，但是这个提案不一定 be chosen 被选定，被选定的提案必须是过半的 Acceptor 通过的提案. 再比如提案这个术语， 在Paxos Made Simple 论文中，Lamport 一开始使用的是抽象的 value 来表示进程们需要达成一致选定的值，值是计算机中常用的术语，不会给人带来太大的困惑，后面必须引入编号时，Lamport 才定义 proposal 提案由编号和 value 组成，这就让读者读起来非常自然。

编号的作用是什么？编号的作用是给提案一个身份标识，Acceptor 通过编号可以记录通过了哪些提案。编号必须是全局唯一的，即不同的 Proposer 提出的提案的编号也必须不一样。不同的Proposer 从不相交的编号集合中选择自己的编号，这样任何两个Proposer就不会用到相同的编号了。每个Proposer都记录（在可靠存储设备中）它使用过的最大编号，然后用比这更大编号的提案开始Phase 1。一个简单的办法，比如有 10 个进程，进程的id设置为0 到9, id 为 m 的进程选择模 10 余 m 的编号，且以10递增编号，这样任何两个Proposer就不会用到相同的编号了。编号还有一个重大作用！它是一个Proposer 们需要抢占的资源，抢占资源的过程就是一场投票的过程，超过半数Acceptor 的投票且编号最高的 Proposer 提出的提案会有可能被过半的 Acceptor 通过. 所以对于特定的 Proposer 来说，编号还必须是单调递增的.

即使提案已经被选定， Proposer 还是可以提出新的提案（比如老的主 Proposer （老 Leader) 崩溃，新的主Proposer（新Leader）不知道提案已经被选定），只不过新 Leader 在阶段1就会学习到选定的 value 值，此时如果新Leader 收到了过半的都带有相同value值的响应，那么此时新 Leader 可以确定 value 值已被选定，否则（带有相同 value 值的响应没有过半，但是响应是过半的, 即有些没有带 value 值或有些带有不同 value 值）要继续阶段2。 所以我对作者在 Implementing a State Machine 一节说的两段话不是很赞同，阶段1 可以优化: (a)Paxos 一致性算法中，被提出的 value 值只在 Phase2 才会被选定。回忆一下，在 Proposer 完成 Phase 1 时，要么提案的 value 值被确定了，要么 Proposer 可以自由提出任意值。 (b)假设执行结果表明，实例 135 和 140 的提案值已被确定，但是其他执行实例的提案值是没有限制的。那么 Leader 可以执行实例 135 和140 的 Phase 2，进而选定第 135 和 140 条命令。

如何为一系列顺序的命令选定 value, 请参考 Implementing a State Machine.

为了理解该paxos 阶段1、阶段2算法，我举了下面的场景。当然这是在没有主 proposer 即没有主 leader 时的讨论.

如下图，P[n1] 代表 prepare 请求编号为 n1, A[n1,v1] 代表 accept 请求编号为 n1, 值为 v1. 其中 P[n1],A[n1,v1] 由 P1 发出，P[n2],A[n2,v2] 由 P2 发出。由于网络原因，导致 A1 先收到 P[n2] 再收到 A[n1,v1],此时A1 显然要拒绝P1的 A[n1,v1] accept 请求，因为 n1 小于 A1 已经响应的prepare 编号 n2. 顺便说下 A[n2,v2] 由于网络丢包没能到达 A1.

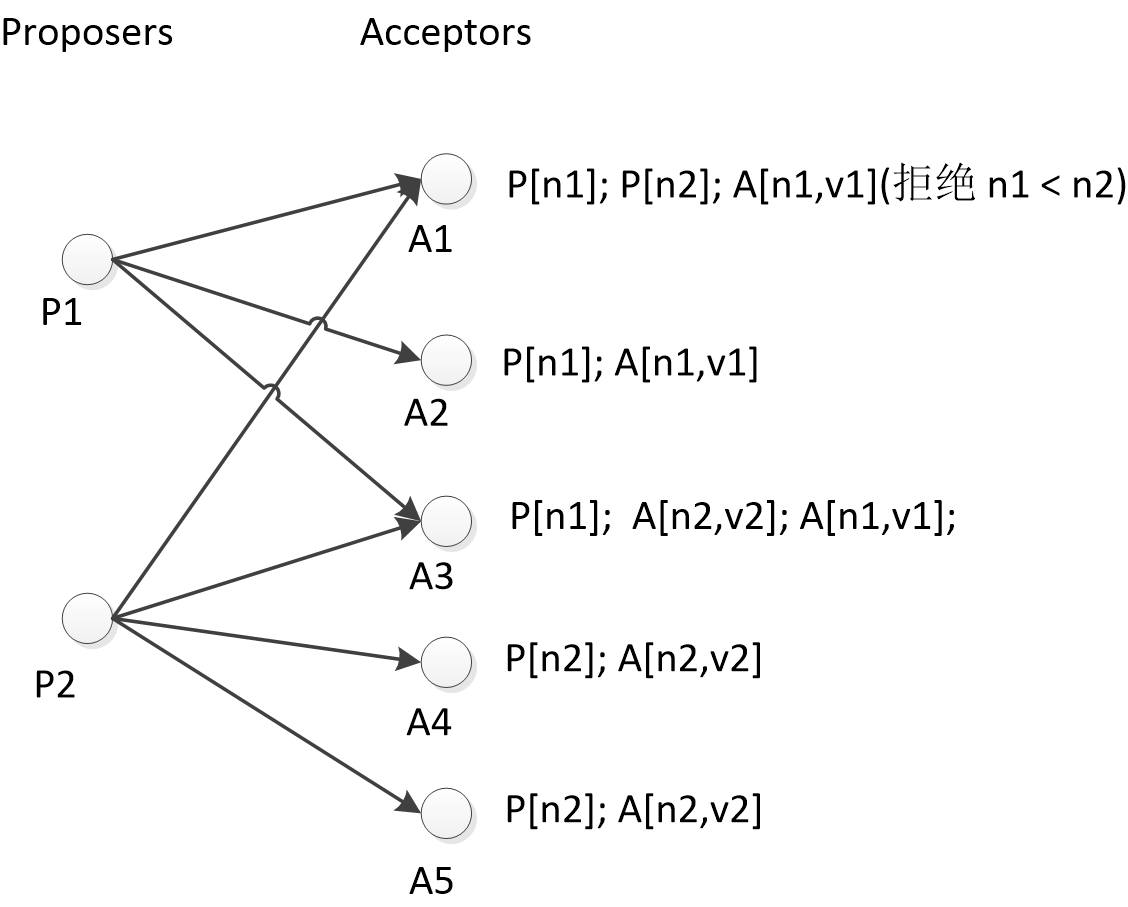
再看 A3, 由于网络原因 P[n2] 丢包了，没有到达 A3,但是 P2 还是收到了过半的P[n2] 响应，所以P2可以发出A[n2,v2], 此时响应中不带value, 所以P2 可以自由选择value . 而 A[n2,v2] 先于 A[n1,v1] 到达A3, 当 A[n2,v2] 到达 A3 时，n2 大于 P[n1] 中的 n1, 所以根据阶段1 的流程，A3 会通过 A[n2,v2] 提案; 当 A[n1,v1] 到达 A3 时n1 等于P[n1]中的 n1，根据阶段1 的流程, A3 还是会通过 A[n1,v1]. A3 通过了一个编号比之前通过的提案编号小的提案，会不会带来问题呢？即会不会导致出现 v1, v2 同时被选定呢？从上图来看，显然是不会的，因为 A1 已经拒绝了A[n1,v1]提案, A[n1,v1] 提案通过的数量不过半。如何严格证明呢？下面我将采用反证法证明。

证明：反证法。由于A[n2,v2]被选定了，那么 P2 必定要发出 A[n2,v2] accept 请求，推出必定存在一个过半的 Acceptors 集合 S 响应了P[n2]请求且不带value 值，同时也可以断定 S 中没有一个Acceptor 会先于P[n2] 响应前通过A[n1,v1] 提案，否则在P[n2] 的响应中将带有 value 值 v1，即 S 中没有一个会通过提案A[n1,v1],因为 n1 小于已经响应的n2. 假设 A[n1,v1] 也被选定，那么必定存在过半的 Acceptors 集合 $S_2$, $S_2$中每一个 Acceptor 都通过了提案A[n1,v1], S 和 $S_2$ 必定有交集，这和前面推出的“S 中没有一个会通过提案A[n1,v1]”结论矛盾，所以假设不成立.

事实上，还可以更严格一些，不存在A[n2,v2]被某些 Acceptor 通过，同时 A[n1,v1]被选定的情况。同样可以使用上面的反证法。由于A[n2,v2]被某些 Acceptor 通过，那么 P2 必定要发出 A[n2,v2] accept 请求，推出必定存在一个过半的 Acceptors 集合 S 响应了P[n2]请求且不带value 值......

但是要注意，A[n2,v2] 被选定，A[n1,v1]被某些 Acceptor 通过（未超过半数） 的情况显然是存在的，上面的图就是一个例子，A[n1,v1] 通过的数量未过半，P[n2] 的请求未能到达已通过 A[n1,v1] 的 Acceptor.