仿射变换可以将矩形转换为平行四边形，可以挤压形状，但是必须保持两边平行。常见的是旋转、缩放、平移变换。缩放和平移比较简单，本文重点推导旋转缩放变换矩阵。

任意一点$(x_0,y_0)$ 可以看成$(x_0, 0)$向量和$(0,y_0)$向量相加，对$(x_0,y_0)$ 绕原点逆时针旋转$\theta$，相当于$(x_0,0),(0,y_0)$ 绕原点逆时针旋转$\theta$ 后的向量相加。

在图像处理中图片的坐标通常使用的是左手坐标系，如下图，x 轴为图片宽度方向，y轴为高度方向。

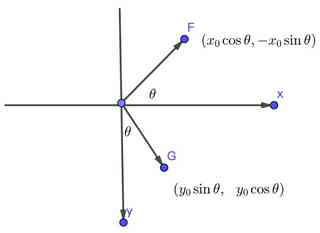
因此 $(x_0, y_0)$ 点逆时针旋转 $\theta$ 后的坐标为 

\begin{align*}   \begin{pmatrix}     x_1 \\     y_1\\   \end{pmatrix}   = (x_0 \cos \theta + y_0 \sin \theta, -x_0\sin \theta + y_0 \cos \theta) =    \begin{pmatrix}   \cos\theta   &  \sin\theta \\   -\sin\theta & \cos\theta   \end{pmatrix}   \begin{pmatrix}     x_0 \\     y_0\\   \end{pmatrix} \end{align*}

旋转矩阵为

\begin{align*}   \begin{pmatrix}   \cos\theta   &  \sin\theta \\   -\sin\theta & \cos\theta   \end{pmatrix} . \end{align*}

上面是绕原点旋转，\textbf{如果是绕任意一点旋转呢？} 假设旋转中心center为 $(c_x, c_y)$。 我们把坐标原点移动到  $(c_x, c_y)$ ，

旧坐标系任意点(x, y)在新坐标系下则为$(x-c_x, y-c_y)$。 因此在新坐标系下绕原点逆时针旋转$\theta$ ，即

\begin{align*}   \begin{pmatrix}     x^*\\     y^*\\   \end{pmatrix} =    \begin{pmatrix}   \cos\theta   &  \sin\theta \\   -\sin\theta & \cos\theta   \end{pmatrix}   \begin{pmatrix}     x-c_x \\     y-c_y \\   \end{pmatrix} \end{align*}

新坐标系下旋转后的点$(x^*, y^*)$在旧坐标系下则为$(x^* + c_x, y^* + c_y)$ 。 因此旧坐标系下绕 $(c_x, c_y)$ 逆时针旋转 $\theta$ 后的点为

\begin{align*}   \begin{pmatrix}     x'\\     y'\\   \end{pmatrix}    =&    \begin{pmatrix}   \cos\theta   &  \sin\theta \\   -\sin\theta & \cos\theta   \end{pmatrix}   \begin{pmatrix}     x-c_x \\     y-c_y \\   \end{pmatrix} +    \begin{pmatrix}     c_x\\     c_y\\   \end{pmatrix} \\   =&    \begin{pmatrix}     \cos\theta x + \sin\theta y - c_x\cos\theta - c_y\sin\theta + c_x   \\     -\sin\theta x  + \cos\theta y + c_x\sin\theta - c_y\cos\theta + c_y \\   \end{pmatrix} \\   =&   \begin{pmatrix}     \cos\theta  &  \sin\theta  &  (1 - \cos\theta)c_x - c_y\sin\theta   \\     -\sin\theta &  \cos\theta &  c_x\sin\theta + (1-\cos\theta)c_y \\   \end{pmatrix}    \begin{pmatrix}     x\\     y\\     1\\   \end{pmatrix}  \end{align*}

现在再考虑缩放，分2种情况:

(1) 旋转后以原点为中心缩放 scale, 记$scale * \cos \theta = \alpha$ , $scale * \sin \theta = \beta$ ，则

\begin{align*}   \begin{pmatrix}     x'\\     y'\\   \end{pmatrix}    =&    \begin{pmatrix}     scale & 0\\     0 & scale  \end{pmatrix}   \begin{pmatrix}     \cos\theta  &  \sin\theta  &  (1 - \cos\theta)c_x - c_y\sin\theta   \\     -\sin\theta &  \cos\theta &  c_x\sin\theta + (1-\cos\theta)c_y \\   \end{pmatrix}    \begin{pmatrix}     x\\     y\\     1\\   \end{pmatrix} \\   =&    \begin{pmatrix}     \alpha  &  \beta  &  (scale - \alpha)c_x - \beta c_y   \\     -\beta &  \alpha &  \beta c_x + (scale-\alpha)c_y \\   \end{pmatrix}    \begin{pmatrix}     x\\     y\\     1\\   \end{pmatrix} \end{align*}

(2) 旋转后以$(c_x, c_y)$ 为中心点缩放，分2步： 第1步，先按上面(1)变换，此时$(c_x, c_y)$点变为了$(scale * c_x, scale * c_y)$ ；第2步 x分量平移 $c_x - scale * c_x$ ，y 分量平移$c_y - scale * c_y$。因此

\begin{align*}   \begin{pmatrix}     x'\\     y'\\   \end{pmatrix}    =&    \begin{pmatrix}     \alpha  &  \beta  &  (scale - \alpha)c_x - \beta c_y   \\     -\beta &  \alpha &  \beta c_x + (scale-\alpha)c_y \\   \end{pmatrix}    \begin{pmatrix}     x\\     y\\     1\\   \end{pmatrix}   +   \begin{pmatrix}   0  &  0  &  c_x - scale * c_x   \\   0 &  0 &  c_y - scale * c_y \\ \end{pmatrix}  \begin{pmatrix}   x\\   y\\   1\\ \end{pmatrix} \\ =& \begin{pmatrix}   \alpha  &  \beta  &  (1 - \alpha)c_x - \beta c_y   \\   -\beta &  \alpha &  \beta c_x + (1-\alpha)c_y \\ \end{pmatrix}  \begin{pmatrix}   x\\   y\\   1\\ \end{pmatrix} \end{align*}

顺便提下，毛星云写的《OpenCV3 编程入门》旋转缩放矩阵是错的，写成了2*1矩阵；《学习OpenCV 3》中文版则有一个符号错误，把加号写成了减号。这2本书都没有推导过程，这也是我写这篇文章的原因。

晚上喝了点小酒，文本有不通顺的地方还请见谅。