B树的定义
B树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树,如下图。B树是Bayer 和 McCreight在1972年提出来的,但是他们并没有解释为什么取名为B树。B树类似于红黑树, 但它们在降低磁盘I/O操作数方面要更好一些。许多数据库系统使用B树或者B树的变种如B+树来存储信息。B树与红黑树的不同之处在于B树的结点可以有很多孩子,从数个到数千个。也就是说,一个B树的“分支因子”可以相当大,尽管它通常依赖于所使用的磁盘单元的特性。B树类似于红黑树,就是每棵含有n个结点的B树的高度为O(log[n])。然而,一棵B树的严格高度可能比一棵红黑树的高度要小许多,这是因为它的分支因子,也就是表示高度的对数的底数可以非常大。因此,我们也可以使用B树在时间O(log[n])内完成一些动态集合的操作。
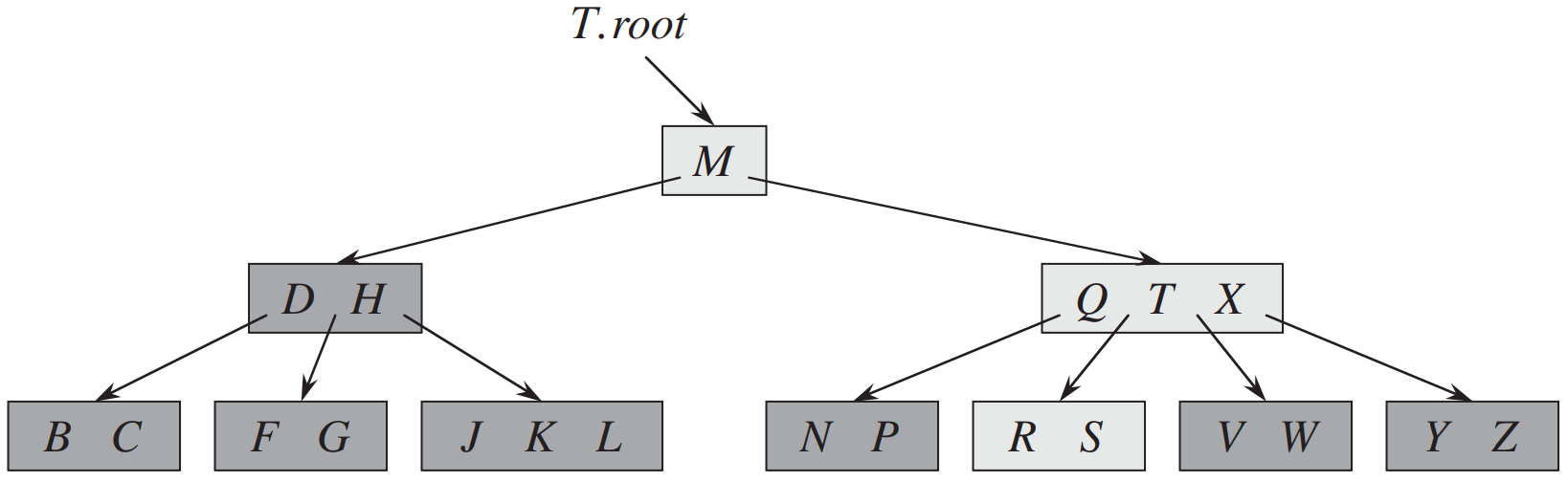
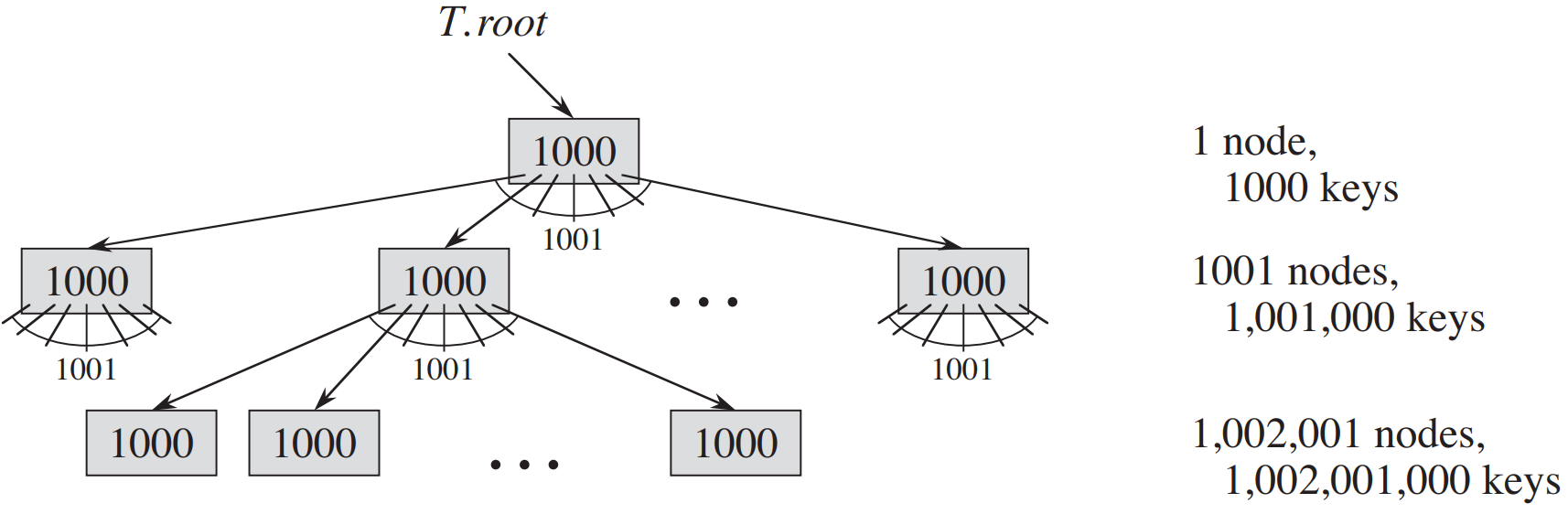
由于在大多数系统中,一个B树算法的运行时间主要由它所执行的DISK-READ和DISK-WRITE操作的次数决定,所以我们希望这些操作能够读或写尽可能多的信息。因此,一个B树结点通常和一个完整磁盘页一样大,并且磁盘页的大小限制了一个B树结点可以含有的孩子个数。一个大的分支因子可以大大地降低树的高度以及查找任何一个关键字所需的磁盘存取次数。下图显示的是一棵分支因子为1001、高度为2的B树,它可以存储超过10亿个关键字。不过,由于根结点可以持久地保存在主存中,所以在这棵树中查找某个关键字至多只需两次磁盘存取。这里只是举例分支为1001的情况,实际上不大可能,因为一般磁盘分页大小为8KB或16KB。按16KB计算,假设1024个分支,那么一个分支只有16个字节,假设在32位系统下,一个key、child分别为4个字节(请参考下面B树的数据结构),再加上数据值字段,很快就超过了16字节。 B+树改进了这一问题,非叶子结点不存储值字段,即使如此对于B+树来说,达到1000个分支也是不太可能的,但是100个分支是普遍的,因为1个分支占160字节(不包含值字段)对于大多数场景来说是足够的。
B树除了根结点以外的每个内部结点(非叶子结点)包含的子树的数目必须大于等于t,这个t被称为B树的最小度数(mininum degree)。但是前一句话并没有说明叶子结点的情况,因为叶子结点没有子树,因此更准确的说法是,除了根结点以外每个结点关键字的数目必须大于等于t-1,这个t被称为B树的最小度数(mininum degree)。
B树的结点的关键字数目为2t-1时,称这个结点是满的,此时无法插入新的关键字,必须进行分裂成2个结点,中间的关键字提升到父结点。这样,分裂后的2个结点的关键字数目就为(2t-2)/2=t-1。删除的时候,我们也需要保证,除了根结点以外,每个结点至少有t-1个关键字。
t值最小为2,即必须满足 t>=2。原因上面一段已经提到,当结点满时,必须分裂成2个结点,中间的关键字提升到父结点,这就要求结点满的时候关键字数目必须 >= 3; 如果 t=1 ,那么结点关键字数目为1时(2t-1=1)就已经满了,此时无法做分裂操作;t=2 时,2t-1=3,刚好满足条件。
B树为什么要设计成,除了根结点以外每个结点关键字的数目必须大于等于t-1 ?这原因是B树的应用场景,前面已经介绍过为了减少磁盘的读取和写入次数,必须尽可能的增大每个结点的分支数目,因为我们希望除了根结点以外每个结点关键字的数目必须大于等于某个我们设定的值。
现在正式给出B树的定义和数据结构,如下:
// 必须满足 t >= 2,
static const int t = 3;
struct Node
{
// 为叶结点则为true,否则为false. 每个叶结点具有相同的深度.
bool isLeaf;
// key 的总数, 除了根结点以外每个结点关键字的数目必须大于等于t-1
int n;
T key[2 * t - 1]; // 按升序排序 key[0]<=key[1]<=...<=key[n-1]
// 关键字对各子树的关键字的范围进行分割;如果k(c[i])为任意存储在子树pChild[i]的关键字, 那么
// k(c[0]) <= key[0] <= k(c[1]) <= ... <= k(c[n-1]) <= key[n-1] <= k(c[n])
Node *pChild[2 * t];
Node(bool b = true, int _n = 0) : isLeaf(b), n(_n) {}
};B树的搜索
和二叉搜索树、红黑树、平衡二叉树的搜索类似,只不过结点中包含多个key,需要增加对结点中key的搜索,这可以通过二分查找算法加快查找速度。
B树的插入
B树中插入一个关键字要比二叉搜索树中插入一个关键字复杂得多。像二叉搜索树中一样, 要查找插入新关键字的叶结点的位置。然而,在B树中,不能简单地创建一个新的叶结点,然后将其插入,因为这样得到的树将不再是合法的B树。相反,我们是将新的关键字插入一个已经存在的叶结点上,因为如果插入到内部结点会破坏key的数目比child少1的性质。由于不能将关键字插入一个满的叶结点,故引入一个操作,将一个满的结点 y(有2t-1个关键字)按其中间关键字(median key)$y.key_t$, 分裂(split)为两个各含t-1个关键字的 结点。中间关键字被提升到y的父结点,以标识两棵新树的划分点。但是如果y的父结点也是满的,就必须在插入新的关键字之前将其分裂, 最终满结点的分裂会沿着树向上传播。 递归向上传播分裂增加了复杂度,于是下面我们将采用另外一个思路,向下查找插入位置的过程中就分裂沿途遇到的每个满结点,避免了向上传播分裂。
与一棵二叉搜索树一样,可以在从树根到叶子这个单程向下过程中将一个新的关键字插入B 树中。为了做到这一点,我们并不是等到找出插入过程中实际要分裂的满结点时才做分裂。相反,当沿着树往下查找新的关键字所属位置时,就分裂沿途遇到的每个满结点(包括叶结点本身)。因此,每当要分裂一个满结点y时,就能确保它的父结点不是满的。
分裂B树中的结点
函数split_child(Node *x, int i)的输入是一个非满的内部结点x(假定在主存中)和一个使$x.c_i$ (也假定在主存中)为x的满子结点的下标i。该函数把这个子结点分裂成两个,并调整x,使之 包含多出来的孩子。要分裂一个满的根,首先要让根成为一个新的空根结点的孩子,这样才能使用split_child(Node *x, int i). 树的高度因此增加1;分裂是树长高的唯一途径。
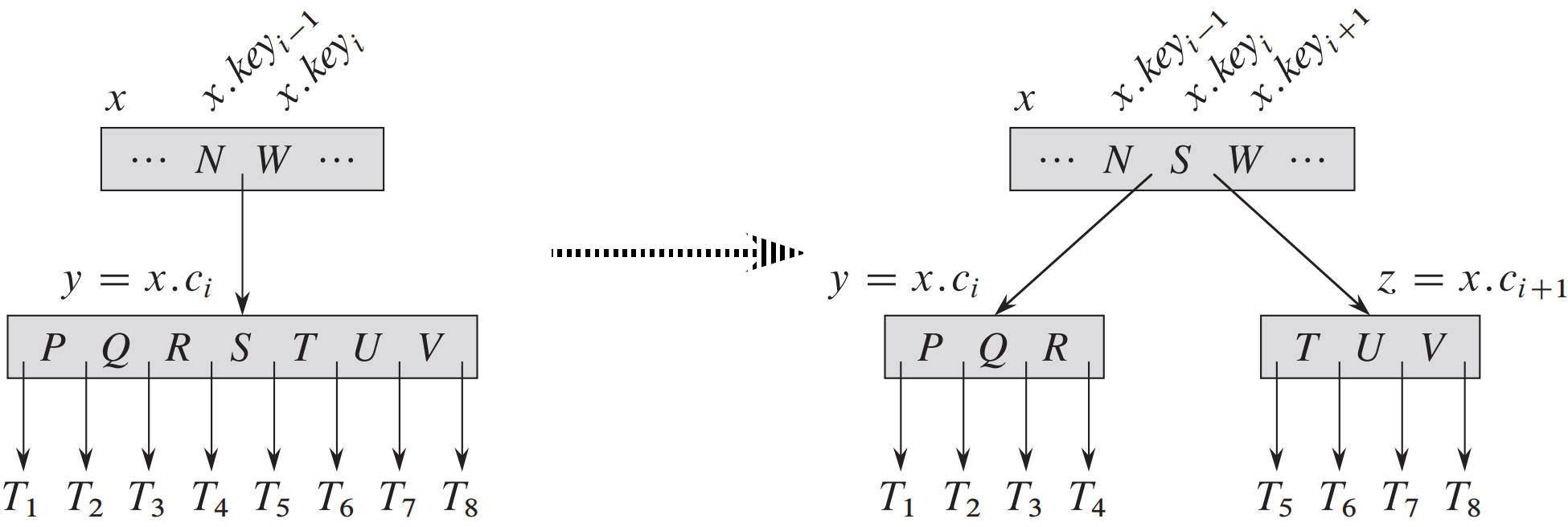
B树的删除
B树上的删除操作与插入操作类似, 必须防止因删除操作而导致树的结构违反B树性质。因为可以从任意一个结点中删除一个关键字,而不仅仅是叶结点,而且当从一个内部结点删除一个关键字时,还要重新安排这个结点的孩子。必须保证一个结点不会在删除期间变得太小(根结点除外,因为它允许有比最少关键字数t-1还少的关键字个数)。一个简单插入算法,如果插入关键字的路径上结点满,可能需要向上回溯;与此类似,一个简单删除算法,当要删除关键字的路径上结点(非根)有最少的关键字个数时,也可能需要向上回溯。
为了方便描述,我们定义当结点的关键字数目达到最少时,即 t-1 时,称之为半满的。
删除过程从以x为根的子树中删除关键字k。和插入类似,为了只需沿树下降一趟,从而避免“向上回溯”,我们设计的这个过程必须保证无论何时,结点x递归调用自身时,x中关键字个数不会破坏至少是半满的性质,我们可以通过一些操作,使得x中的关键字个数至少为最小度数t,即超过半满的。这个加强的条件允许在一趟下降过程中,就可以将一个关键字从树中删除,无需任何“向上回溯”。当要删除某个内部结点的关键字时,该过程也要沿树下降一趟(请参考下面代码 case2.a 和 case2.b 的情况), 用其前驱或后继来取代被删除的关键字。
由于一棵B树中的大部分关键字都在叶结点中,我们可以预期在实际中,删除操作最经常用于从叶结点中删除关键字。这样删除过程只要沿树下降一趟即可,不需要向上回溯。尽管这个过程看起来很复杂,但对一棵高度为h的B树,它只需要O(h)次磁盘操作,因为在递归调用该过程之间,仅需O(1)次对DISK-READ和DISK-WRITE的调用。所需CPU时间为$O(th)=O(t log_t n)$ 。
//递归的删除关键字
void recursive_remove(Node *pNode, const T &key)
{
int i = 0;
while (i < pNode->n && key > pNode->key[i])
++i;
if (i < pNode->n && key == pNode->key[i]) // 关键字key在结点pNode中
{
// case1. 关键字key在叶结点中。
// 由case3可知,pNode必定是超过半满的 n>=t, 因此可以放心的删除 k,不会破坏至少是半满的性质
if (pNode->isLeaf) //pNode是个叶结点
{
// 从pNode中删除k
delete_at(pNode, i);
return;
}
else // case2. 关键字key在个内部结点中
{
// case2.a case2.b 通过前驱或后继替换被删除的关键字,这样pNode的孩子可以保持不变。
// 之所以pChildPrev或pChildNext必须满足超过半满的,这是因为在递归删除前驱或后继关键字时,
// 有可能导致pChildPrev或pChildNext的关键字数量减1,这便可以保证不会破坏至少是半满的性质。
Node *pChildPrev = pNode->pChild[i]; // 结点pNode中前于key的子结点
Node *pChildNext = pNode->pChild[i + 1]; // 结点pNode中后于key的子结点
if (pChildPrev->n >= t) // case2.a. 结点pChildPrev超过半满
{
T prevKey = get_predecessor(pChildPrev); //获取key的前驱关键字
recursive_remove(pChildPrev, prevKey);
pNode->key[i] = prevKey; // 替换成key的前驱关键字
return;
}
else if (pChildNext->n >= t) // case2.b. 结点pChildNext超过半满
{
T nextKey = get_successor(pChildNext); //获取key的后继关键字
recursive_remove(pChildNext, nextKey);
pNode->key[i] = nextKey; //替换成key的后继关键字
return;
}
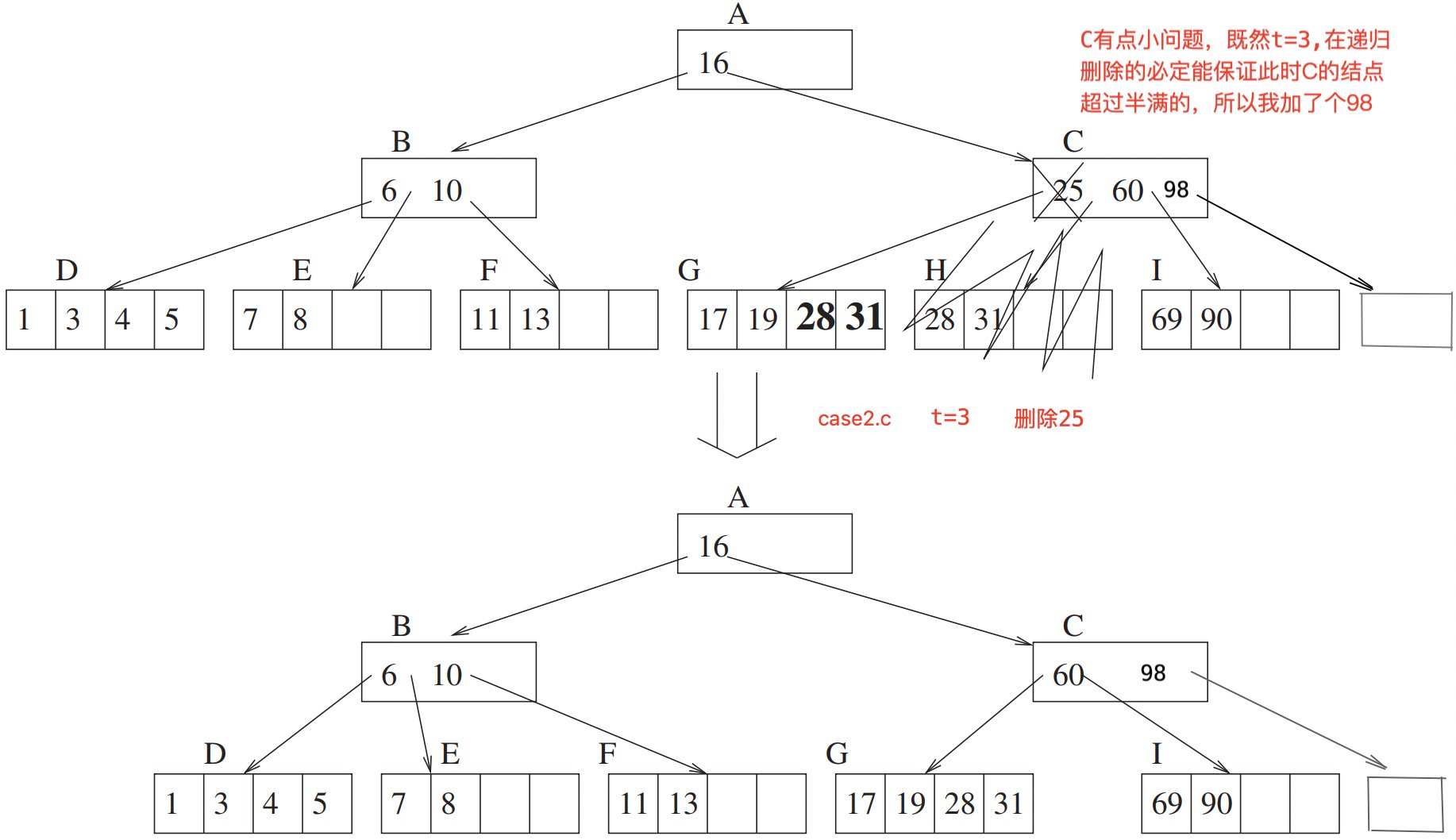
else // case2.c. 结点pChildPrev和pChildNext中恰好都是半满的
{
// 由case3可知,pNode必定是超过半满的 n>=t, 因此合并孩子后,pNode 的 key 也在
// merge_child()中被删除了(合并到孩子结点上了),可以放心,pNode 不会破坏至少是半满的性质
merge_child(pNode, i);
recursive_remove(pChildPrev, key);
}
}
}
// case3. 关键字key不在结点pNode中,并且不是叶子结点。这里我增加了不是叶子结点的判断
// 由于外部调用保证了 key 一定存在,所以这个不是叶子结点的判断虽然是多余的,但是为了这个
// 函数自身的健壮性,仍然加上这个判断。
else if (!pNode->isLeaf)
{
Node *pChildNode = pNode->pChild[i]; //包含key的子树根结点
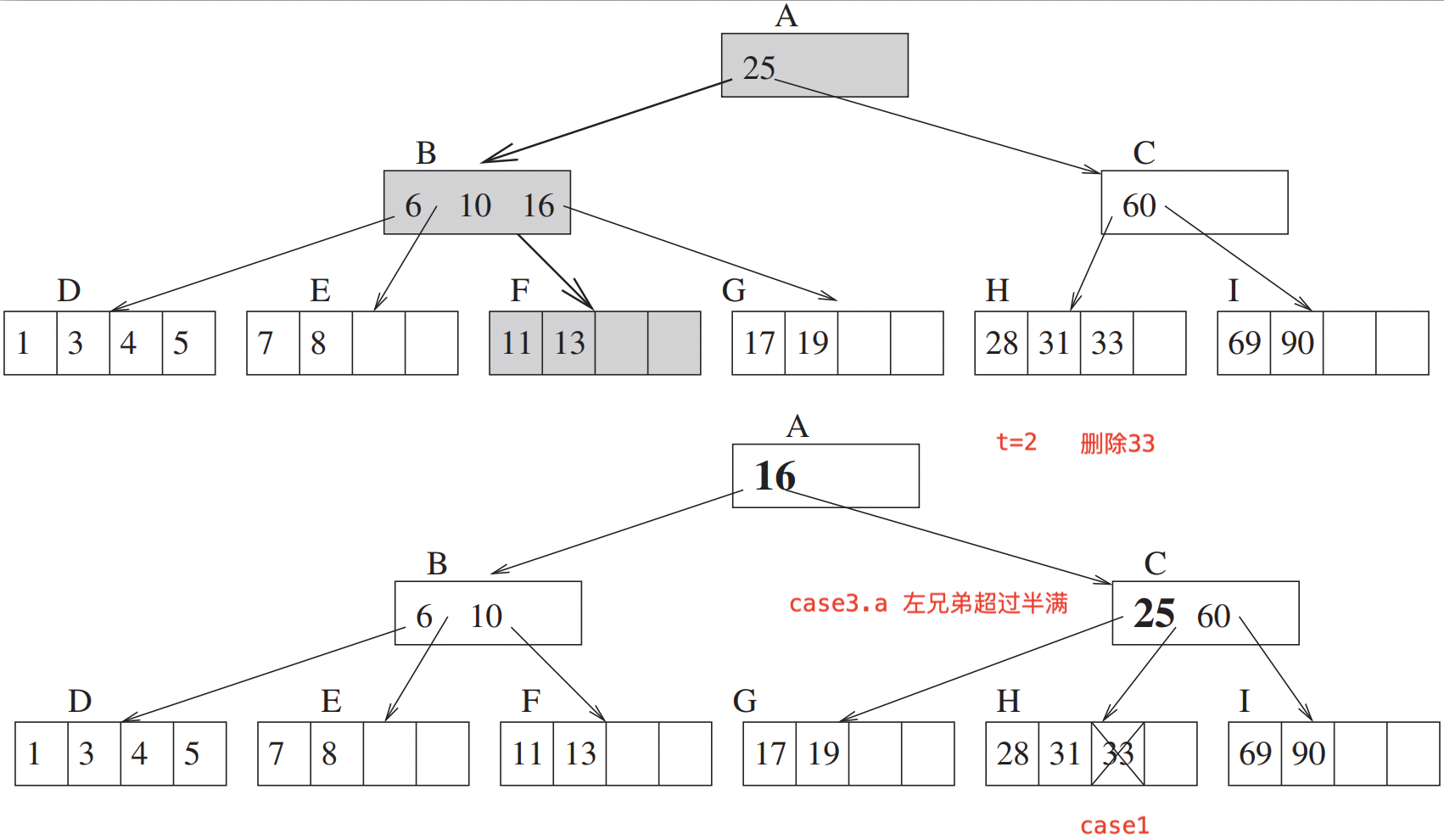
// case3.a y=x.[i], y 刚好半满,需要通过左右兄弟结点z和父结点x相应的关键字移动和下沉,
// 使得y超过半满。原因是递归删除的时候,y有可能因为 case3.b 导致y的1个结点被下沉到y孩子的合并结点,
// 所以必须使得y超过半满。
if (pChildNode->n == t - 1) //恰好是半满的
{
Node *pLeft = i > 0 ? pNode->pChild[i - 1] : NULL; //左兄弟结点(i==0,无左兄弟)
Node *pRight = i < pNode->n ? pNode->pChild[i + 1] : NULL; //右兄弟结点(i==n,无右兄弟)
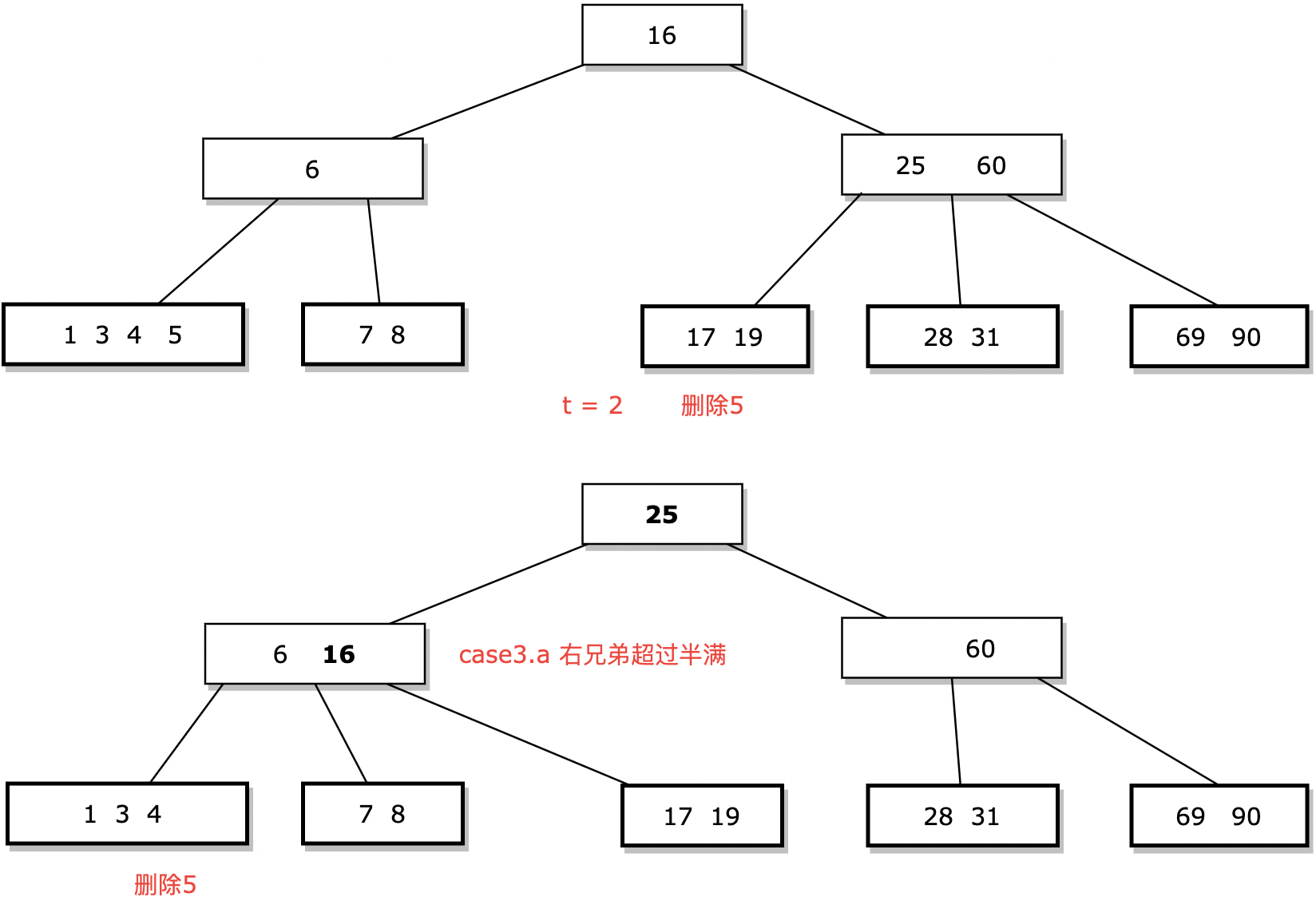
// case3.a 若左(右)兄弟超过半满(n>=t)
if (pLeft && pLeft->n >= t) //左兄弟节超过半满
{
// 父结点中i-1的关键字下移至pChildNode第1个关键字;
// 把左兄弟结点最后1个child移动到 pNode 的第1个结点,如果不是叶子结点的话。
insert_at(pChildNode, 0, pNode->key[i - 1], pLeft->isLeaf ? nullptr : pLeft->pChild[pLeft->n]);
//pLeft结点中的最大关键字上升到pNode中, 注意pNode的位置是i-1, 而右兄弟结点时是i
pNode->key[i - 1] = pLeft->key[pLeft->n - 1];
--pLeft->n;
}
else if (pRight && pRight->n >= t) //右兄弟超过半满
{
//父结点中i的关键字下移至pChildNode中
pChildNode->key[pChildNode->n] = pNode->key[i];
++pChildNode->n;
//pRight结点中的最小关键字上升到pNode中, 注意pNode的位置是i, 而左兄弟结点时是i-1
pNode->key[i] = pRight->key[0];
if (!pRight->isLeaf)
{
// 把右兄弟结点第1个child移动到 pChildNode 的最后1个结点
pChildNode->pChild[pChildNode->n] = pRight->pChild[0];
}
delete_at(pRight, 0);
}
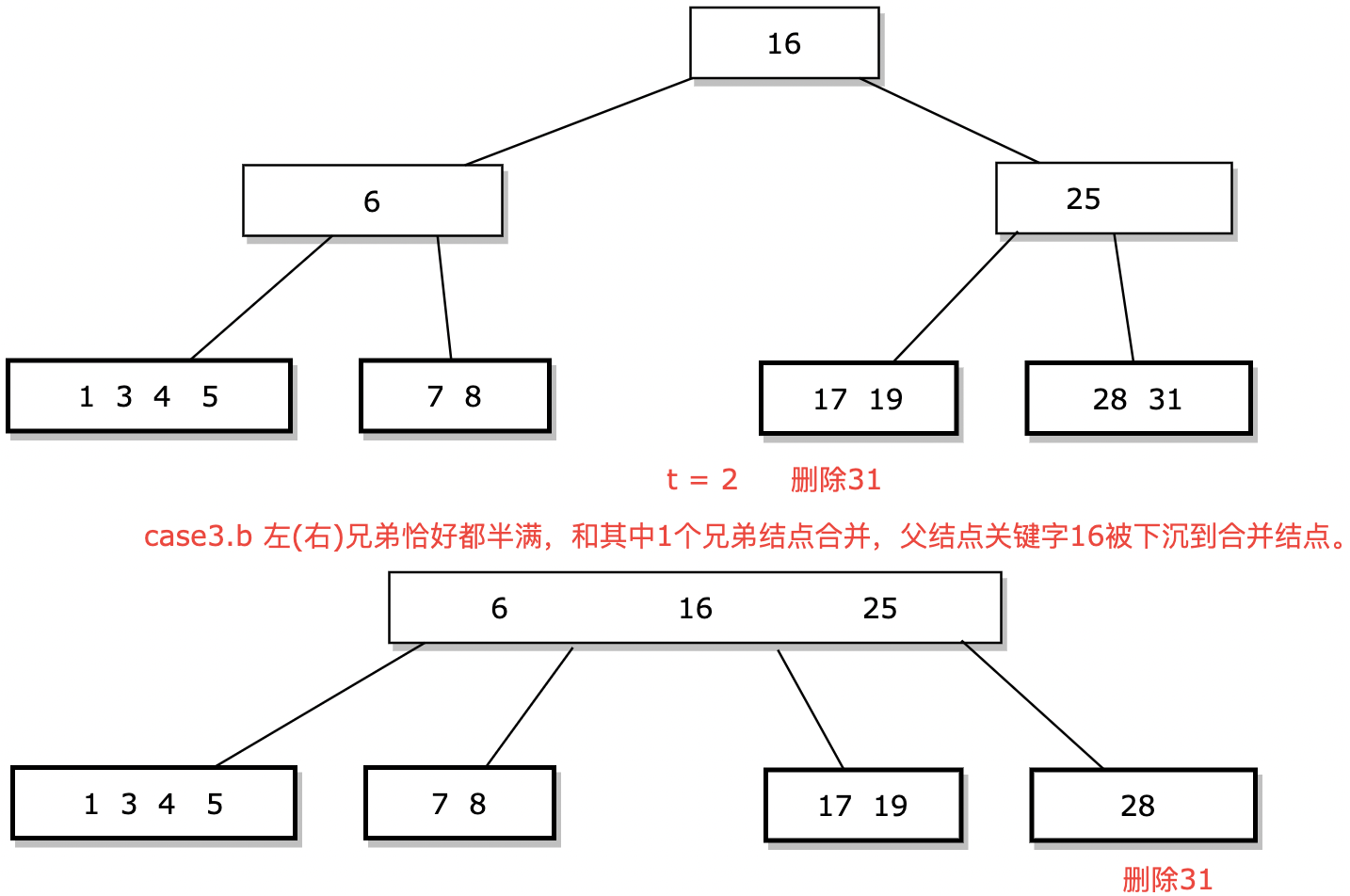
// case3.b 左(右)兄弟恰好都半满,和其中1个兄弟结点 y 合并,父结点pNode[i-1](pNode[i])
// 被下沉到合并结点。放心,由于case3 可以断定父结点pNode是超过半满的,不会破坏至少是半满的
// 性质: 除非pNode是根结点, 此时有可能会发生坍缩,树的高度减1。
else if (pLeft) //与左兄弟合并
{
merge_child(pNode, i - 1);
pChildNode = pLeft;
}
else if (pRight) //与右兄弟合并
{
merge_child(pNode, i);
}
}
recursive_remove(pChildNode, key);
}
// else 到达叶子, key 不存在的情形
}
B+树
B+树(B+-tree)是B树种最著名、应用最广泛的一种变种。与B树有两个主要区别:
1. 首先,B+树中的所有值都保存在叶结点中。
2. 其次,所有叶结点都作为一个双向链表链接在一起。
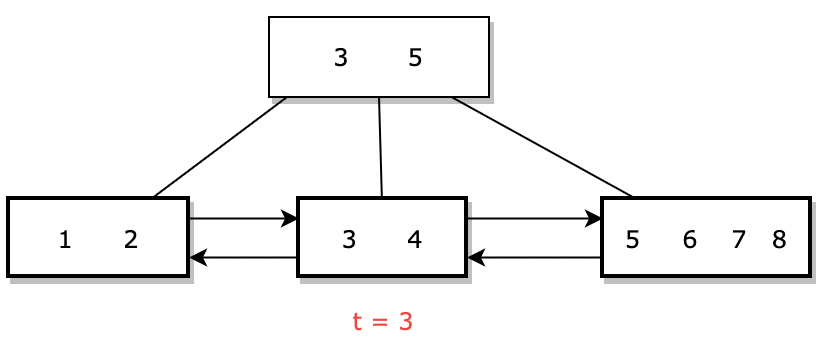
如下图,B+树的结构看起来与B树非常相似。在B+树的索引结点中,与B树不同,我们不存储值,但存储关键字。但是,由于所有值都存储在叶结点,因此索引结点中存储的关键字充当路由器,搜索时根据它们转到正确的孩子结点。
B+树搜索
与B树一样,B+树支持精确匹配搜索,该搜索查找具有给定关键字的对象。此外,B+树可以很好的支持范围搜索,可以查找关键字位于给定范围内的所有值。
为了执行精确的匹配搜索,B+树遵循从根到叶的单一路径,和B树不同,B树如果在索引结点找到关键字,即停止搜索,而B+树必须到叶子结点才能结束。
B+树能很好的支持范围搜索的原因在于,B+树将所有值都存储在叶子结点中,并且把叶结点通过双向循环链表链接在一起。如果我们想搜索其关键字在范围R=[low,high]内的所有值,我们将对key=low执行精确匹配搜索。当我们到达叶结点l时。我们可以通过二分查找列表,找到对应的key,然后对列表右边的关键字依次校验,如果关键字 < high 则继续,如果达到列表尾部还未结束,则继续跳到该叶结点的下一个兄弟结点,依此类推。当遇到关键字 >high的对象时,算法停止。如果 key 允许重复,则我们还需要向列表和链表的左边方向进行搜索,直到关键字 < low 。
B+树插入
由于B+树中的所有值都位于叶子结点,我们基本上按照精确匹配搜索来查找叶子结点,然后我们将对象插入叶结点。由于B树插入时,总是将新结点插入到叶子结点,因此B+树的插入基本上和B树是类似的。
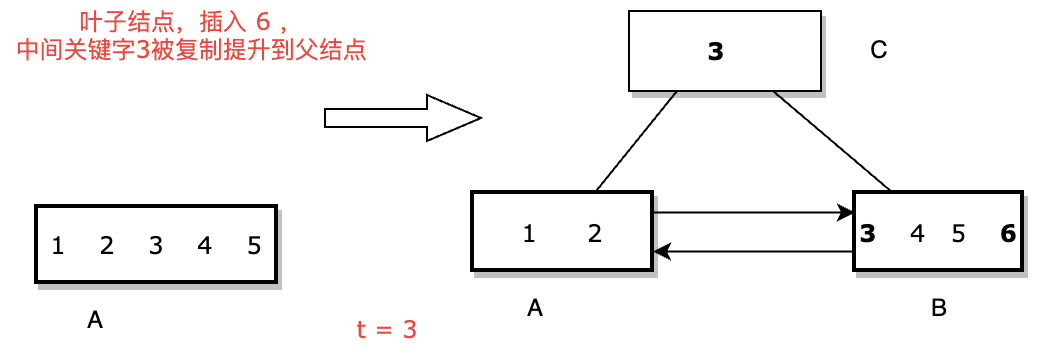
需要注意的是当叶结点满的时候,结点将被分裂成两部分时。在下图中,如果我们尝试在结点A已满时将6对象插入结点A,它会溢出。为了处理溢出,该结点会被分裂为两个结点A和B,其中左A结点key个数为t-1,右B结点个数为t, 比A多1个中间关键字,保证搜索时相等的key,优先走右分支。中间关键字3被复制提升(copied up)到父结点C(和B树类似,只不过B+树是直接提升到父结点)。图中由于A是树根,因此将生成一个新结点C,C成为了新树根。
和B树类似,当中间关键字被复制提升到父结点,也即索引结点时,索引结点也可能满了,它同样需要被分成两部分,这和B树是一样的,中间关键字被提升(pushed up)到父结点。如果父结点也是满的, 就必须在插入新的关键字之前将其分裂, 最终满结点的分裂会沿着树向上传播。在最坏的情况下,分裂将沿插入路径的所有结点。如果根结点一分为二,则树的高度将增加1。
和B树类似,我们并不是等到找出插入过程中实际要分裂的满结点时才做分裂。相反, 当沿着树往下查找新的关键字所属位置时, 就分裂沿途遇到的每个满结点。因此, 每当要分裂一个满结点时, 就能确保它的父结点不是满的。当然当在叶子结点发生分裂时,我们还需要注意维护叶子结点之间的链表。
B+树删除
我看了一些资料,它们介绍的B+树删除算法都是先搜索到叶子结点,删除后,判断是否不足半满的(下溢),如果发生下溢则向左右兄弟结点借或合并的方式,避免下溢,合并的时候需要向上递归。我思考后,其实B+树的删除可以和上面B树的删除类似,不需要向上递归,只需要沿树向下下降一趟即可。和上面B树的删除基本是类似的,但是需要注意到下面2点。我已经编码验证测试没有问题。
1. B树删除 case2(关键字key在个内部结点中) 中,会使用前驱或后继的关键字替换删除的关键字, 或者合并左右孩子。但是B+树必须搜索到叶子结点才能进行删除。因此当为 case2 时,要当作 case3(关键字key不在结点中)处理, 按 case3 走 child[i+1] 的分支(其中 key[i] 和要删除的关键字相等)。
2. case3(关键字key不在结点中),如果包含key的子树根结点y超过半满的,和B树一样向下递归删除。如果y恰好是半满的: (2.1) 若y是索引结点,和B树一样处理; (2.2)若y是叶子结点: (2.2.1) 如果左(右)兄弟超过半满,则从左(右)兄弟借一个过来到y,把借的key复制提升覆盖父结点对应的key(右兄弟时是借的key的下一个key);(2.2.2) 如果左(右)兄弟恰好半满,y和其中1个兄弟合并,和B树不同的是父结点对应的key不是下沉,而是直接删除,当然还应注意维护叶子结点的链表关系。
